Qual das alternativas apresenta a matriz que roda os vetores do por um ângulo (no sentido trigonométrico, isto é, anti-horário):
Passo 1
Como vimos na teoria, temos:
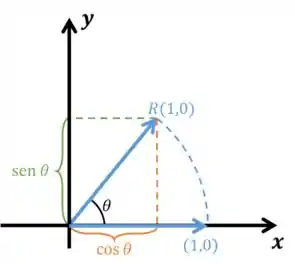
Portanto,
Logo,
Resposta
Letra
Exercícios de Livros Relacionados
Os pontos A ( 2 , - 1 ) e B ( - 1 ,4 ) são vértices consecutivos de um quadrado. Calcular os outros dois vértices, utilizando a matriz-rotação.
O vetor v = ( 3 ,2 ) experimenta sequencialmente:1) Uma reflexão em torno da reta y = x ;2) Um cisalhamento horizontal da fetor 2 ;3) Uma contração na direção O y de fator 1 3 ;4) Uma rotação de 90 °
Determinar, em cada caso, a matriz da transformação linear de R 2 em R 2 que representa a sequência de transformações dadas.Rotação de 30 ° no sentido horário, seguida de uma duplicação dos módulos e
Determinar, em cada caso, a matriz da transformação linear de R 2 em R 2 que representa a sequência de transformações dadas.Reflexão em torno da reta y = - x , seguida de uma dilatação de fator 2 na d
Determinar, em cada caso, a matriz da transformação linear de R 2 em R 2 que representa a sequência de transformações dadas.Rotação de 60 ° , seguida de uma reflexão em relação ao eixo dos y .