Em um triângulo , os ângulos e medem cada. Sendo e , determinar o vértice .
Passo 1
Beleza, temos esses pontos:
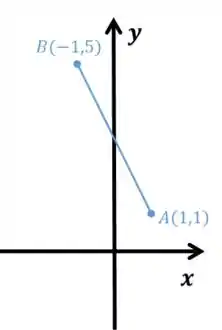
Bom, sabemos que o ângulo em e em valem . Logo, temos um triângulo isósceles com os lados e iguais.
Além disso como a soma dos ângulos internos de um triângulo é , o ângulo em vale . Logo, basta rodarmos em torno de de um ângulo de :
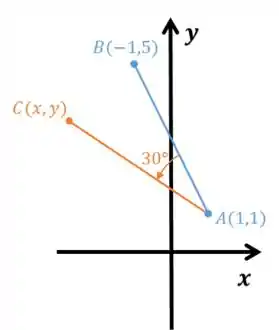
Onde,
Chegamos na equação:
Temos então:
O que implica em:
Encontramos o ponto
Passo 2
Chegamos assim ao nosso triângulo:
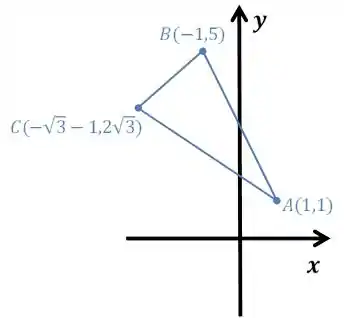
Se tivéssemos rodado para o outro lado, chegaríamos ao triângulo:
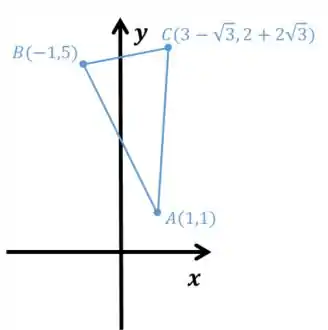
Resposta
ou
Exercícios de Livros Relacionados
Os pontos A ( 2 , - 1 ) e B ( - 1 ,4 ) são vértices consecutivos de um quadrado. Calcular os outros dois vértices, utilizando a matriz-rotação.
O vetor v = ( 3 ,2 ) experimenta sequencialmente:1) Uma reflexão em torno da reta y = x ;2) Um cisalhamento horizontal da fetor 2 ;3) Uma contração na direção O y de fator 1 3 ;4) Uma rotação de 90 °
Determinar, em cada caso, a matriz da transformação linear de R 2 em R 2 que representa a sequência de transformações dadas.Rotação de 30 ° no sentido horário, seguida de uma duplicação dos módulos e
Determinar, em cada caso, a matriz da transformação linear de R 2 em R 2 que representa a sequência de transformações dadas.Reflexão em torno da reta y = - x , seguida de uma dilatação de fator 2 na d
Determinar, em cada caso, a matriz da transformação linear de R 2 em R 2 que representa a sequência de transformações dadas.Rotação de 60 ° , seguida de uma reflexão em relação ao eixo dos y .