Exercícios Resolvidos de Matriz Rotação

Enunciado

Os pontos e são vértices consecutivos de um quadrado. Calcular os outros dois vértices, utilizando a matriz rotação.

Passo 1

Antes de começarmos, é bom frizar que não é necessário nenhum conhecimento especial pra fazer esse problema haha. Vou botar as imagens pra vocês verem o que tá acontecendo mas não seria necessário!

Bom, temos o seguinte:

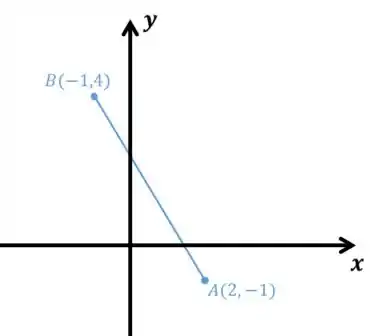
Para acharmos outro vértice através da rotação podemos girar em torno de de ! Então, temos que:

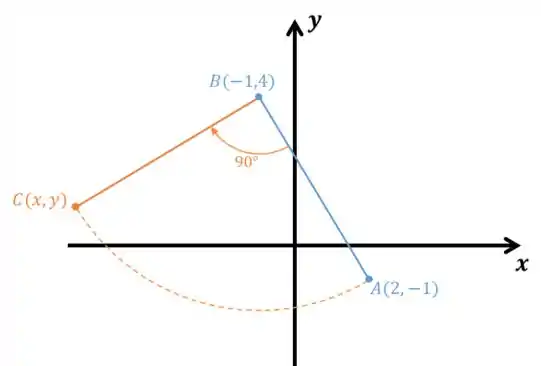
Onde,

Obs: Cuidado com o sinal dos senos! Nesse caso estamos girando no sentido horário, então o sinal fica no seno de baixo.

Chegamos na equação:

Temos então:

O que implica que:

Encontramos o ponto

Passo 2

Agora vamos achar o vértice do quadrado! Para isso, vamos girar em torno de no sentido anti-horário:

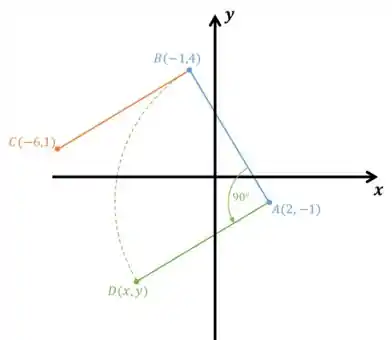
Onde,

Resolvendo a equação:

Dessa forma,

Logo,

Portanto, temos

Passo 3

E está pronto nosso quadrado ;)

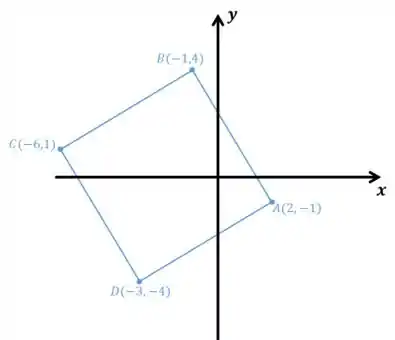
Alternativamente, poderíamos rodado para o outro lado, de forma que encontraríamos o quadrado:

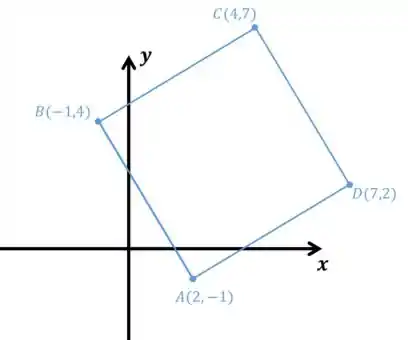
Resposta

e ou e

Exercícios de Livros Relacionados

Os pontos A ( 2 , - 1 ) e B ( - 1 ,4 ) são vértices consecutivos de um quadrado. Calcular os outros dois vértices, utilizando a matriz-rotação.

O vetor v = ( 3 ,2 ) experimenta sequencialmente:1) Uma reflexão em torno da reta y = x ;2) Um cisalhamento horizontal da fetor 2 ;3) Uma contração na direção O y de fator 1 3 ;4) Uma rotação de 90 °

Determinar, em cada caso, a matriz da transformação linear de R 2 em R 2 que representa a sequência de transformações dadas.Rotação de 30 ° no sentido horário, seguida de uma duplicação dos módulos e

Determinar, em cada caso, a matriz da transformação linear de R 2 em R 2 que representa a sequência de transformações dadas.Reflexão em torno da reta y = - x , seguida de uma dilatação de fator 2 na d

Determinar, em cada caso, a matriz da transformação linear de R 2 em R 2 que representa a sequência de transformações dadas.Rotação de 60 ° , seguida de uma reflexão em relação ao eixo dos y .