Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Medidas de Dispersão para V.A. Multidimensionais

Ver Teoria
Exercício 123456789101112131415

Enunciado

Considere a distribuição conjunta de X e Y, conhecida, dada na tabela abaixo.

Considerando X e Y independentes.

b) Calcule as médias de X, Y e XY

d) Calcule a variância de X,Y e X+Y

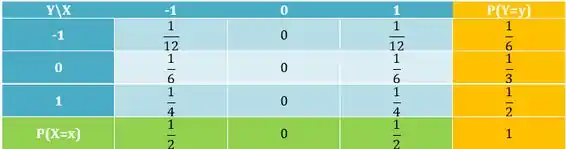
Passo 1

Sabemos que

E X = ∑ x . P ( X = x )

Portanto

E X = ∑ i = - 1 1 x i . P X = x i = - 1 . 1 2 + 0 . 0 + 1 . 1 2 = 0

E Y = ∑ j = - 1 1 y j . P Y = y j = - 1 . 1 6 + 0 . 1 3 + 1 . 1 2 = 1 3

Passo 2

Para calcular E(XY) usaremos

E X Y = ∑ x i y j P ( X = x i , Y = y j )

E X Y = - 1 - 1 1 12 + - 1 0 0 + - 1 1 1 12 + 0 - 1 1 6 + 0 0 0 + 0 1 1 6 + 1 - 1 1 4 + 1 0 0 + 1 1 1 4 = 0

Passo 3

Para o cálculo da Var(X) precisamos lembrar da seguinte fórmula:

V a r X = E X 2 - E X 2

Portanto precisamos calcular E ( X 2 )

E X 2 = - 1 2 1 2 + 0 2 0 + 1 2 1 2 = 1

E Y 2 = - 1 2 1 6 + 0 2 1 3 + 1 2 1 2 = 2 3

Substituindo na fórmula teremos

V a r X = 1 - 0 2 = 1

V a r Y = 2 3 - 1 3 2 = 5 9

Passo 4

Para calcular Var(X+Y) usaremos

V a r X + Y = V a r X + V a r Y + 2 . C o v ( X , Y )

C o v X , Y = E X , Y - E X . E ( Y )

Vamos lá!

C o v X , Y = 0 - 0.1 3 = 0

V a r X + Y = 1 + 5 9 + 2 × 0 = 14 9

Resposta

E X = 0

E Y = 1 3

E X Y = 0

V a r X = 1

V a r Y = 5 9

V a r X + Y = 14 9

Exercícios de Livros Relacionados

Numa sala estão cinco crianças cujas idades são (em anos): 3, 3, 4, 5, 5. Escolhem-se três crianças ao acaso para formar uma trinca. X indica a idade da mais nova da turma, e Y à da mais velha. Calcul
Suponha que X seja uma variável aleatória contínua com distribuição de probabilidades f X ( x ) = x 18 ,0 ≤ x ≤ 6 Encontre a distribuição de probabilidades da variável aleatória Y=2X+10Encontre o valo
Considere que os pesos de indivíduos sejam independentes e normalmente distribuídos, com uma média de 160 libras e um desvio padrão de 30 libras. Suponha que 25 pessoas se espremam em um elevador proj
Suponha que X seja uma variável aleatória com distribuição de probabilidade f X ( X ) = 1 4 para 1,2,3,4Encontre a distribuição de probabilidade de Y=2X+1
Uma variável aleatória X tem a seguinte distribuição de probabilidades: f X ( x ) = e - x , x ≥ 0 Encontre a distribuição de probabilidades para Y=X^2Encontre a distribuição de probabilidades para Y=X