Numa urna têm-se cinco bolas marcadas com os seguintes números: -1, 0, 0, 0, 1. Retiram-se três bolas, simultaneamente: X indica a soma dos números extraídos e Y o maior valor da trinca. Calcule:
b) E(X) e Var(X)
c) E(X,Y)
Passo 1
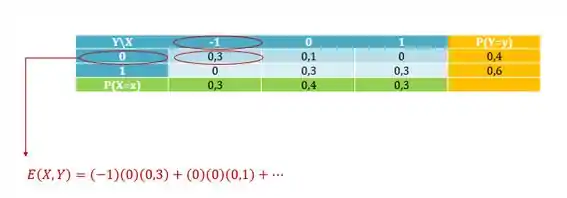
Montamos a tabela de distribuição em um exercício anterior lembram? (Exercício de Fixação 2 – Tipo Introdução à Probabilidade Conjunta):
Y\X
-1
0
1
P(Y=y)
0
0,3
0,1
0
0,4
1
0
0,3
0,3
0,6
P(X=x)
0,3
0,4
0,3
Vamos calcular agora E(X)
Passo 2
Calculando Var(X)
Para isso precisamos calcular
Portanto
Passo 3
Agora precisamos calcular E(XY). Pela tabela é fácil, saca só:
Resposta
Exercícios de Livros Relacionados
Numa sala estão cinco crianças cujas idades são (em anos): 3, 3, 4, 5, 5. Escolhem-se três crianças ao acaso para formar uma trinca. X indica a idade da mais nova da turma, e Y à da mais velha. Calcul
Suponha que X seja uma variável aleatória contínua com distribuição de probabilidades f X ( x ) = x 18 ,0 ≤ x ≤ 6 Encontre a distribuição de probabilidades da variável aleatória Y=2X+10Encontre o valo
Considere que os pesos de indivíduos sejam independentes e normalmente distribuídos, com uma média de 160 libras e um desvio padrão de 30 libras. Suponha que 25 pessoas se espremam em um elevador proj
Suponha que X seja uma variável aleatória com distribuição de probabilidade f X ( X ) = 1 4 para 1,2,3,4Encontre a distribuição de probabilidade de Y=2X+1
Uma variável aleatória X tem a seguinte distribuição de probabilidades: f X ( x ) = e - x , x ≥ 0 Encontre a distribuição de probabilidades para Y=X^2Encontre a distribuição de probabilidades para Y=X