A barra curva tem uma massa por unidade de comprimento. Determine o momento do peso da barra em relação ao ponto
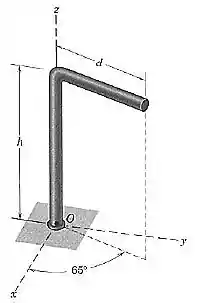
Passo 1
Vamos aplicar o momento calculado de forma vetorial nesse problema.
Primeiro, vamos dividir a estrutura em duas barras: uma barra vertical de comprimento e outra barra horizontal de comprimento . A força peso de cada uma dessas barras será:
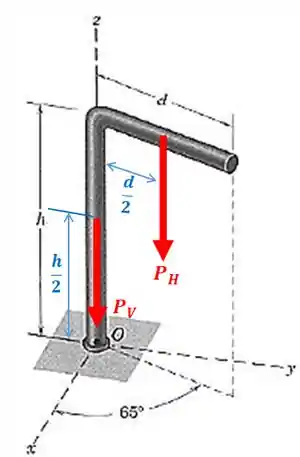
Onde, é o peso da barra horizontal e é o peso da barra vertical.
Perceba que o peso sempre aponta pra baixo, ou seja, na direção negativa de
Sendo assim, o peso da barra vertical não exerce momento com relação ao ponto , já que a linha de ação do peso desta barra intercepta o ponto
Dessa forma, só a parte horizontal da barra exercerá momento. Essa parte tem o peso dado por:
Passo 2
Agora vamos definir o vetor :
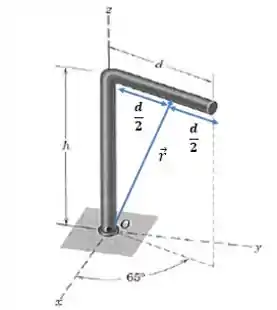
Pela figura, as componentes de são:
Passo 3
O momento será dado por:
Então:
Repare que o último determinante, o que está acompanhado de , é nulo. Calculando os outros:
Arrumando isso e substituindo o valor do cosseno e do seno de