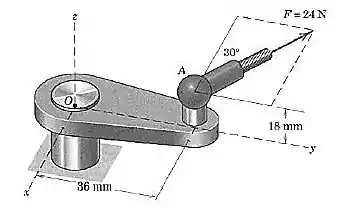
A força de está aplicada ao ponto do conjunto de suportes. Determine o momento dessa força em relação ao ponto
Passo 1
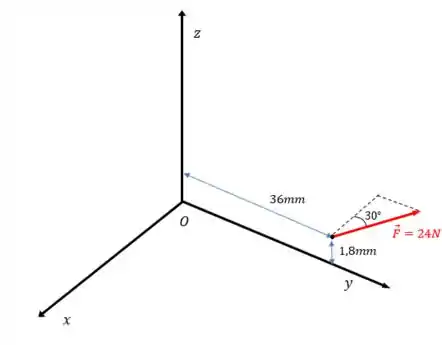
Vamos desenhar o sistema sem os corpos:
Passo 2
De acordo com a figura, podemos definir o vetor por:
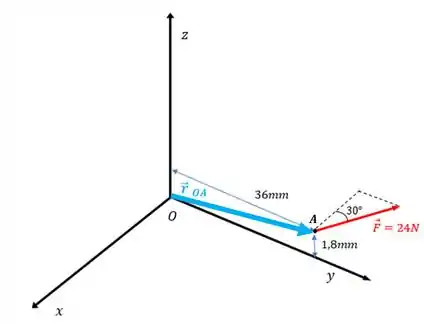
Agora precisamos definir a força. Pela figura, a força faz um ângulo de com o sentido negativo do eixo
Assim:
Passo 3
Agora, pra calcular o momento, vamos usar o nosso velho amigo produto vetorial:
Desenvolvendo: