Determine o momento da força em relação ao ponto
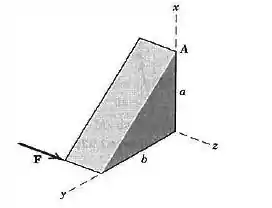
Passo 1
Vamos primeiro escrever o vetor
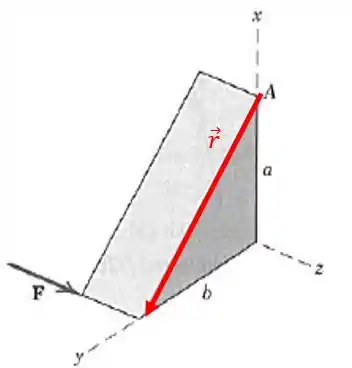
O vetor pode ser escrito como a diferença entre um ponto inicial e um final, sendo esses:
Assim:
Passo 2
E a força ? Pela figura, dá pra perceber que ela é paralela ao eixo e aponta no sentido positivo do mesmo. Sendo assim:
Passo 3
Agora vamos escrever o nosso produto vetorial que representa o momento:
Vamos ter que: