O tubo em ângulo reto é visto abaixo. Substitua a força trativa de que o cabo exerce no ponto por um sistema força binário no ponto
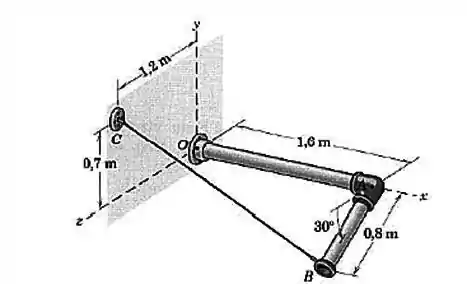
Passo 1
Bom, sabemos que a força atua no ponto através da reta que une .
Além disso, como a força é trativa, o vetor da força terá o sentido indo de para
Como já fizemos antes, o vetor que representa é dado por:
Observando a figura, vemos que:
Se liga: os eixos não estão colocados nos lugares de costume.
Já o ponto é um pouquinho mais complicado pois vamos ter que trabalhar com seno e cosseno. Dá uma olhada: o comprimento faz um ângulo de com a horizontal.
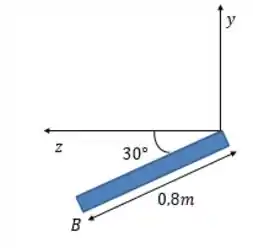
Sendo que a coordenada disso daí é . Então:
Passo 2
Assim:
Passo 3
Então:
Passo 4
Assim, a força é dada por:
Passo 5
Vamos calcular o momento que essa força exerce em . Usando a distância
Assim, o momento será dado por:
Passo 6
Beleza, calculando a força resultante e o momento da força em relação a , você já tem o binário.
O sistema força binário é formado por: