As duas forças que atuam nos cabos das chaves de grifo formam um binário Expresse o binário como um vetor.
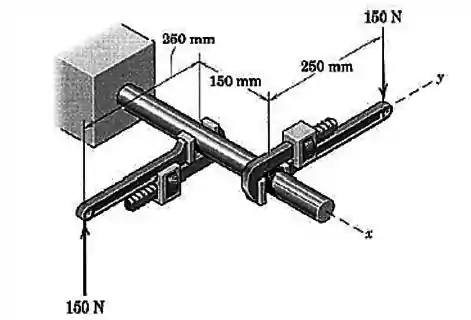
Passo 1
Nessa questão nós vamos fazer diferente: vamos dividir esse problema tridimensional em dois problemas bidimensionais.
Vamos chamar de e de os pontos onde cada força atua no sistema. Assim, visto de cima, temos:
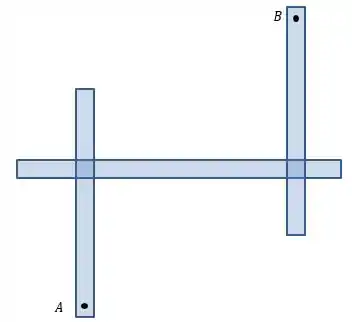
E visto de frente:
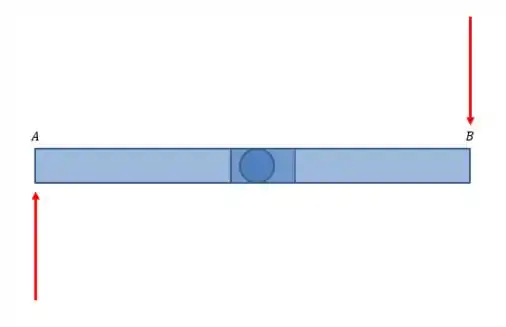
Show?
O que vamos fazer é o seguinte: calcular o módulo de cada uma das componentes do vetor momento total e depois definir o sentido e a direção dessas componentes usando a regra da mão direita.
Passo 2
Colocando os eixos e as distâncias na figura da vista de cima:
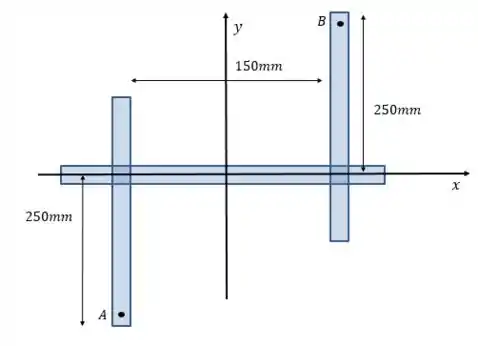
Não dá para ver as forças nessa vistas porque elas são perpendiculares à tela. Mas da figura do enunciado, você consegue saber que a força que atua em aponta para fora da tela e a que atua em atua para dentro.
Além disso, a distância entre as forças é de , assim, o binário é dado por:
Qual a direção desse vetor momento? Bora usar a regra da mão direita:
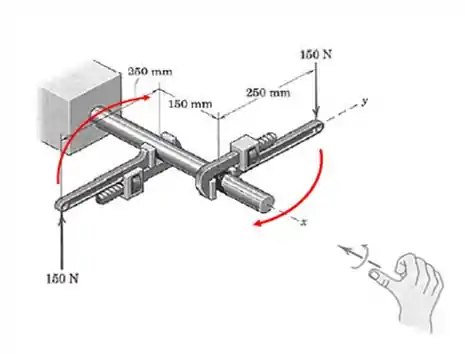
Pela regra, o vetor aponta na direção negativa de . Assim:
Bora calcular a outra componente.
Passo 3
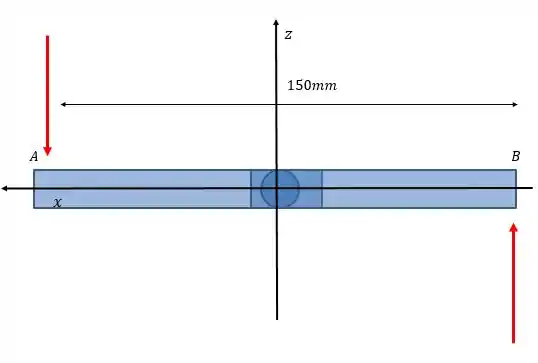
Fazendo a mesma coisa de antes, mas agora com relação ao eixo :
Repare que uma das forças não tem braço de alavanca com relação ao eixo , então o seu momento é nulo.
E pra determinar o sentido? Regra da mão direita:
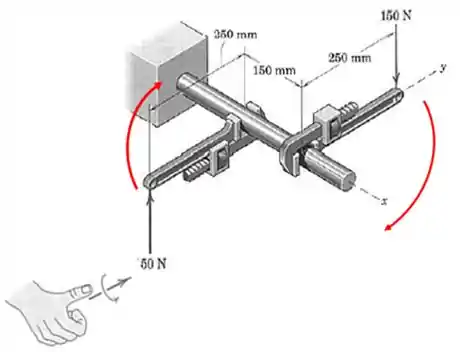
Dá pra ver que essa componente aponta na direção positiva de , né? Assim:
Passo 4
O vetor momento binário será dado por: