Determine o momento da força de em relação ao ponto
- Usando a relação do produto vetorial.
- Projetando a força em seus componentes e achando os seus respectivos momentos.
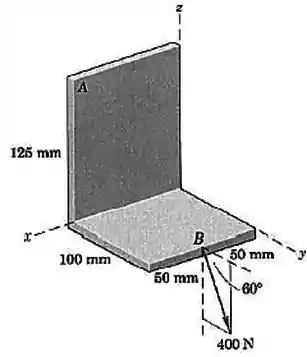
Passo 1
De forma vetorial:
Primeiro, vamos definir o vetor .
Passo 2
Agora vamos definir a força:
Feito isso, podemos calcular o produto vetorial:
Assim:
Passo 3
Para fazer o próximo item, vamos primeiro calcular as componentes da força:
Passo 4
Vamos analisar cada eixo e ver quais forças exercem momento em cada um desses:
Eixo
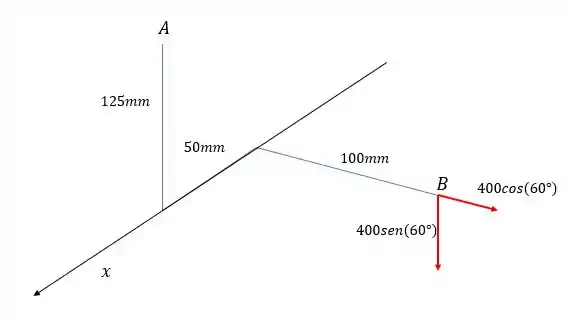
A força de faz um momento no sentido horário, já a outra componente um momento no sentido anti-horário. Tomando o sentido anti-horário como positivo, vamos ter que:
Escrevendo vetorialmente:
Vamos checar se esse sentido é o certo? Bom, o momento é horário, já que é negativo:
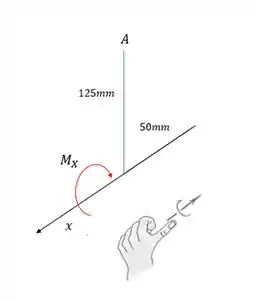
Pela regra da mão direita, o sentido é realmente negativo em Então escrevemos certo!!!
Passo 5
Eixo
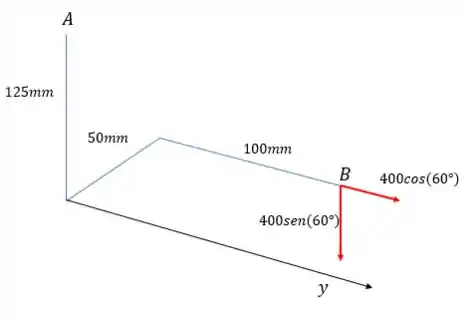
Nesse caso, só a componente vertical realiza momento, pois a componente horizontal é paralela ao eixo . Assim:
E o sentido? Bom, dá para ver que o sentido de rotação, nesse caso, é o horário. Sendo assim, usando a regra da mão direita:
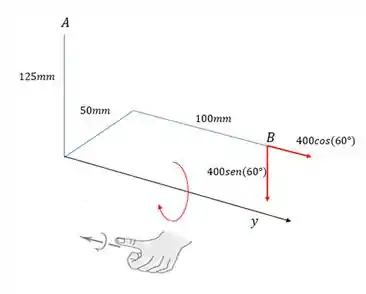
Assim, o sentido do vetor momento é contrário ao sentido positivo do eixo , então:
Passo 6
Eixo :
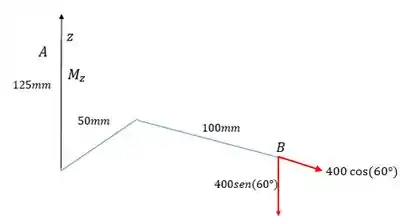
Em relação ao eixo , só a força horizontal exerce momento, pois a força vertical é paralela ao eixo . O momento é nesse sentido aqui:
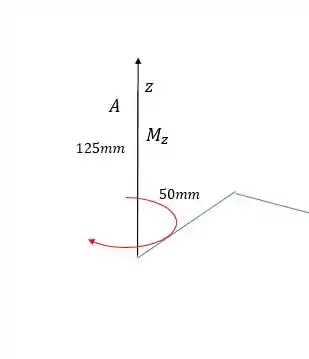
Assim:
Para ver o sentido, vamos usar a regra da mão direita:
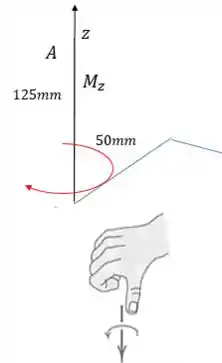
Assim, o vetor momento aponta no sentido negativo de . Então:
E por fim: