Um helicóptero está mostrado e são dadas certas coordenadas tridimensionais. Durante um teste no solo, uma força aerodinâmica de é aplicada ao rotor de cauda , como mostrado. Determine o momento desta força em relação ao ponto da fuselagem.
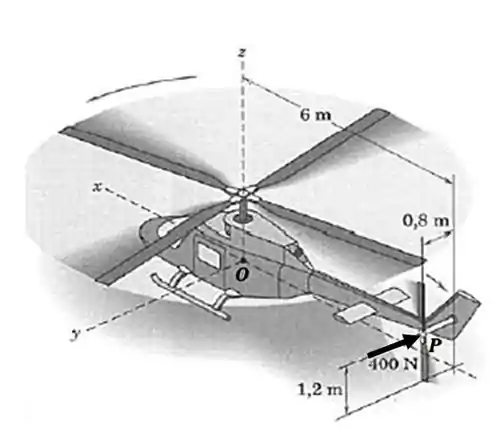
Passo 1
Vamos desenhar esse sistema sem o helicóptero, afinal de contas ele atrapalha um pouquinho a nossa visualização, né?
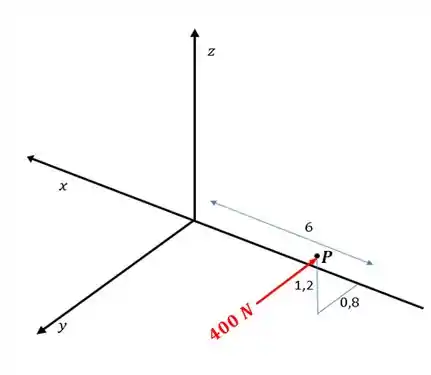
Ou seja, a força está sendo aplicada no ponto:
Então, o vetor distância do ponto até o ponto é dado por:
E a força? Bom, pelo desenho do enunciado, a força é paralela ao eixo , no sentido negativo do mesmo. Então, teremos esse carinha aqui:
Passo 2
Show de bola! Temos tudo para calcular o nosso momento:
Então, vamos ter que:
O determinante do centro, que tem como unitário o , vai ser nulo, assim:
Sacou? É aquele mesmo passo a passo de sempre: define o vetor , depois define o vetor e, por fim, joga no determinante do produto vetorial.