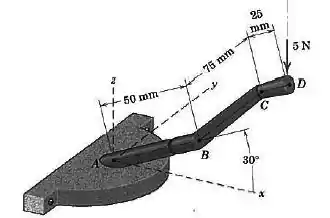
Uma força vertical de é aplicada à manete do mecanismo de abertura de janelas quando a manivela está na horizontal. Determine o momento da força em relação ao ponto e em relação à linha .
Passo 1
Vamos primeiro calcular o momento em relação ao ponto . Para isso, como de costume, vamos desenhar o sistema sem esses corpos:
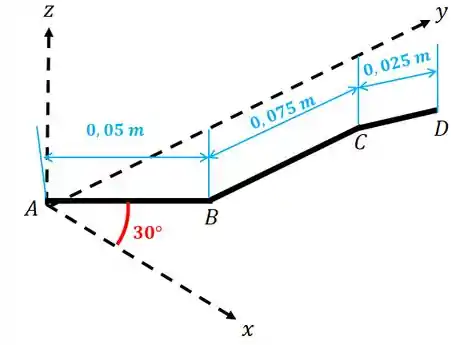
Perceba uma coisa: o trecho é paralelo ao eixo e aponta para dentro da tela. Note também que a força é paralela ao eixo e aponta no sentido negativo do mesmo:
Vamos escrever o vetor .
Mas esse trecho é todo torto, concorda? De até ele é de um jeito, de até de outro e de até de outro.
Podemos, então, escrever como uma soma de três vetores posição:
Para encontrar as componentes de , apenas use cosseno e o seno pra calcular as componentes e
O trecho , pelo contrário, só tem uma componente positiva que aponta na direção positiva de
E o trecho você faz que nem o . Esse trecho possui a mesma inclinação que o trecho
Somando os vetores:
Somando as componentes:
Passo 2
Tudo pronto para calcularmos o nosso momento:
Expandindo:
Perceba que o último determinante dá zero. Calculando os outros:
Passo 3
Show de bola. Agora queremos saber o valor desse momento em relação à linha
O que isso significa? Ah, isso nada mais é do que a projeção do momento naquela direção: a direção
Assim, calcularemos:
Ou seja, o produto escalar entre o momento e o vetor normalizado da direção , que nos dá o módulo da projeção, vezes o próprio vetor .
No final das contas, isso dada mais é do que o nosso produto:
Então, vamos ter que calcular esse vetor .
Passo 4
Não se preocupe, é fácil achar esse . Isso porque já calculamos antes o , então é só normalizar ele:
O módulo deste vetor é:
Então, o vetor unitário vai ser:
Passo 5
Show de bola! Já sabemos que , então:
Vamos escrever esse produto de uma maneira mais fácil de visualizar o que está acontecendo. Algumas componentes ali são nulas, e só podemos fazer o produto termo a termo e entre termos iguais:
Agora que temos que sabemos que:
Podemos escrever este momento como um vetor multiplicando seu módulo pelo vetor unitário: