Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Momentos em Três Dimensões

Ver Teoria
Exercício 81234567910111213

Enunciado

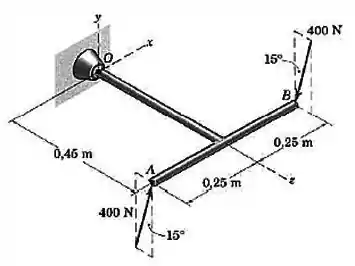
Determine o momento associado ao par de forças de 400   N aplicado à estrutura em T .

Passo 1

Nós vamos resolver essa questão da seguinte forma: calculando o momento de cada uma das forças e depois somando:

M → = M → 1 + M → 2

Passo 2

O momento é em relação ao ponto médio da placa. Desta forma, precisamos calcular os vetores posição r → O A e r → O B :

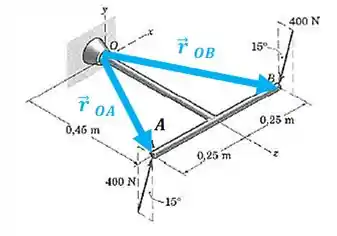
Então, para o vetor posição r → O A , vamos ter:

r → O A = O A → = - 0.25,0 , 0.45

E para o vetor posição r → O B , vamos ter:

r → O B = O B → = 0.25,0 , 0.45

Agora só falta definir as forças. Olhando pra figura, vemos que o ângulo que as forças fazem com o eixo y é de 15 ° . Assim:

F → 1 = F → A = 0 i ^ + 400 c o s 15 ° j ^ + 400 s e n 15 ° k ^

∴

F → 1 = 386,37 j ^ + 103,53 k ^   N

F → 2 = F → B = 0 i ^ - 400 c o s 15 ° j ^ - 400 s e n 15 ° k ^

∴

F → 2 = - 386,37 j ^ - 103,53 k ^   N

Passo 3

Assim, os momentos são calculados segundo os seguintes produtos vetoriais:

M → 1 = r → O A × F → 1 = i ^ j ^ k ^ - 0.25 0 0.45 0 386.37 103.53

Então, para M → 1 :

M → 1 = 0 0.45 386.37 103.53 i ^ - - 0.25 0.45 0 103.53 j ^ + - 0.25 0 0 386.37 k ^

∴

M → 1 = - 173,87 i ^ + 25,89 j ^ - 96,59 k ^     N ⋅ m

Para M → 2 :

M → 2 = r → O B × F → 2 = i ^ j ^ k ^ 0.25 0 0.45 0 - 386.37 - 103.53

M → 2 = 0 0.45 - 386.37 - 103.53 i ^ - 0.25 0.45 0 - 103.53 j ^ + 0.25 0 0 - 386.37 k ^

∴

M → 2 = 173,87 i ^ + 25,89 j ^ - 96,59 k ^     N ⋅ m

Portanto:

M → = M → 1 + M → 2 = - 173,87 i ^ + 25,89 j ^ - 96,59 k ^ + 173,87 i ^ + 25,89 j ^ - 96,59 k ^

∴

M → = 0 i ^ + 51,78 j ^ - 193,18 k ^   N ⋅ m

Resposta

M → = 51,78 j ^ - 193,18 k ^

Exercícios de Livros Relacionados

39. Determine o momento resultante produzido pelas duas forças em relação ao ponto O. Expresse o resultado como um vetor cartesiano.
Um mecânico aplica a força horizontal de 100N perpendicularmente à chave de boca, como indicado na figura. Determine o momento dessa força em relação ao centro do parafuso em O . A linha de centro da
Determine a expressão vetorial para o momento M → O da força de 600N em relação ao ponto O . A especificação de projeto para o parafuso em O necessitaria deste resultado.
A chave especial mostrada é usada para parafusos de difícil acesso que tem uma especificação de baixo torque. Determine o momento da força de 40N aplicada no ponto A do cabo da chave em relação a O .
Uma força de 320N é aplicada à extremidade da chave, quando a polia dentada é presa a biela de um motor. A força é perpendicular ao plano contendo os pontos O , A e B . Determine o momento dessa força