Determine o momento da força em relação ao ponto .
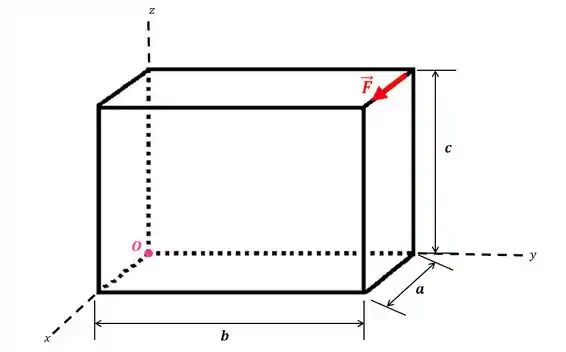
Passo 1
Vamos resolver essa questão usando o produto vetorial, porque os cálculos ficam muito mais simples.
Então, o nosso primeiro passo é determinar o vetor posição que começa no ponto e chega até qualquer ponto da linha de atuação da força:
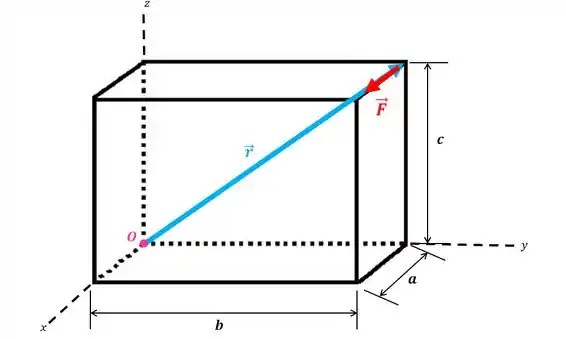
Então, o vetor posição será:
Passo 2
A força só tem componente no eixo e podemos escrever sua forma vetorial assim:
Pronto! Agora é só fazermos o produt vetorial:
Esse determinante fica: