Para reduzir o momento indesejável em relação ao eixo , um mecânico usa sua mão esquerda para sustentar o cabo da chave no ponto . Que força direcionada para cima, , deve ser exercida para que não haja momento em relação ao eixo ? Qual é, então, o momento resultante em relação a
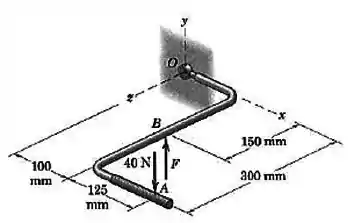
Passo 1
Podemos resolver esse problema dividindo-o em problemas bidimensionais.
A primeira coisa que precisamos descobrir é qual é a força necessária que deve ser aplicada em para que não haja momento em relação a . Ou seja:
Vamos desenhar o esquema das forças nesse caso, baseando-se no nosso enunciado é:
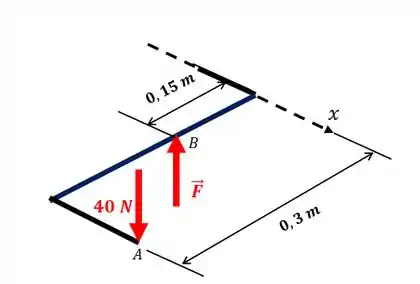
Pronto! Desenhamos o que nos interessa.
Perceba que cada força produzirá um momento em sentido contrário ao outro. Sendo que a força de produz um momento no sentido positivo do eixo , pela regra da mão direita. E o força , que queremos saber, produz um momento negativo:
Pronto, matamos metade da questão.
Passo 2
Agora queremos saber o momento resultante em relação a .
Em primeiro lugar: não existe momento em relação ao eixo , já que as forças são paralelas a esse eixo. Também vimos que o momento resultante em relação a é nulo, então nos resta saber o momento em relação ao eixo
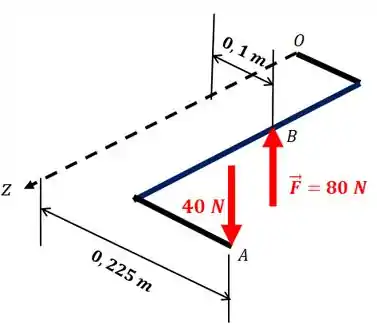
Pela figura, o sentido anti-horário é o positivo. Então, o módulo do momento em é:
Escrevendo de forma vetorial:
Ou: