UFMG, Sem Campus, Fundamentos de Oscilações e Ondas, Listas de Ondas - UFMG - Problemas sobre Oscilador Harmônico, Questão 15
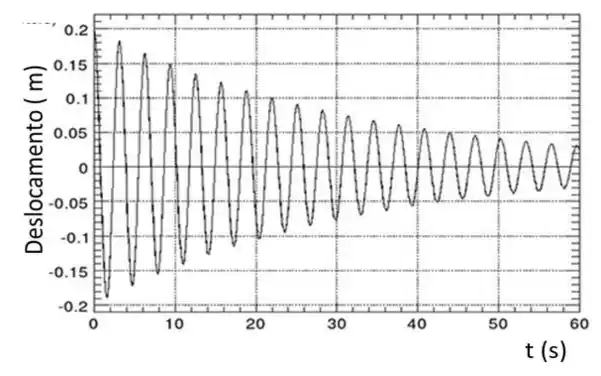
Através de uma força de , um oscilador harmônico amortecido é deslocado de da sua posição de equilíbrio. Em ele é solto (do repouso) e começa a oscilar. O movimento é então registrado como mostrado no gráfico abaixo. Faça uma estimativa, mais precisa que você conseguir, dos valores do período e da massa.
Passo 1
Eaew, belezinha?
Temos aqui um oscilador harmônico amortecido, usando uma força
foi causado um deslocamento de
Após esse deslocamento, soltamos o corpo para oscilar e começamos a contar o tempo, obtendo o gráfico da posição pelo tempo como
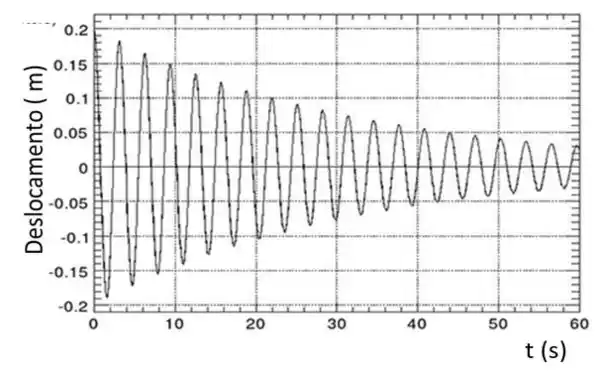
Será que essas informações são o suficiente para determinar a massa da partícula que está presa à mola e o período de oscilação? Nosso problema é regido pela equação diferencial
Pelo gráfico podemos dizer que este é um amortecimento subcrítico! Vamos usar as definições de e para determinar as grandezas desejadas! Saca só!
Passo 2
Temos as seguintes definições
e
e, temos a seguinte relação entre as duas grandezas
A solução para o amortecimento subcrítico é tal que
pelo gráfico temos que e , portanto, obtemos que
Vamos analisar primeiramente a distensão inicial da mola!
Passo 3
Inicialmente, temos que
de forma que
Essa era a informação mais simples de obter! Por isso fiz ela primeiro! Agora, temos uma segunda informação que pode ser obtida diretamente, mas para isso, vamos precisar analisar um pouco mais o sistema! Note que a amplitude máxima é sempre obtida quando
e, nestas situações, a atenuação da amplitude pode ser mensurada usando a relação
Observando o gráfico, temos que para aproximadamente
a amplitude é simplesmente
ou seja, metade da amplitude original, de forma que
aplicando a exponencial de ambos os lados, temos que
Vamos ver o que mais conseguimos dizer sobre este sistema!!
Passo 4
A frequência é aproximadamente o número de ciclos realizados por intervalo de tempo, vamos tentar avaliar essa quantidade! Se observarmos os gráficos podemos perceber que são realizados aproximadamente três ciclos a cada , ou seja, temos aproximadamente intervalos entre picos em um . Desta maneira, podemos garantir que a frequência é tal que
de forma que a frequência angular é dada por
e o período, simplesmente
Usando , e obtidos, temos que
nos leva à
ou simplesmente
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
e