Considere dois osciladores harmônicos idênticos com constantes de mola e acoplados por uma mola muito fraca com constante . A variação na frequência de vibração do modo antissimétrico com relação ao modo simétrico vale aproximadamente?
Passo 1
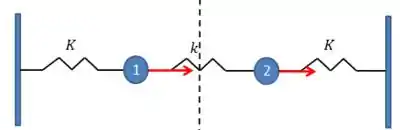
O sistema pode ser representado pela figura abaixo:
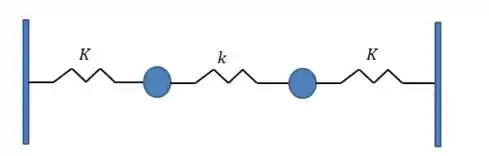
Passo 2
Bom, o enunciado cita dois modos de vibração: o simétrico e o antissimétrico. Vamos seguir o passo a passo para achar as frequências dos modos de vibração.
Primeiro, vamos adotar deslocamentos positivos e para as massas:
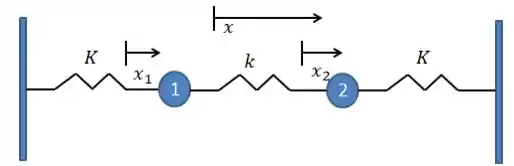
Considerando que , a mola central estará sendo esticada e o módulo da força elástica que a mesma gerará nas massas será:
O sentido das forças em cada massa será:
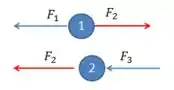
Passo 3
Bora escrever as EDO’s agora, usando o sentido adotado para cada força:
Para a massa 1:
Para a massa 2:
Reescrevendo e isolando
Passo 4
Usando as soluções padrões:
Substituindo e lembrando que:
Assim:
Cortando todos os cossenos:
Passo 5
Escrevendo o sistema na forma matricial:
Como não queremos a solução trivial, o determinante da matriz acima tem que ser nulo:
Assim:
E:
A frequência do modo simétrico será o menor e a frequência do modo assimétrico é a maior:
O modo simétrico apresenta deslocamentos nas extremidades simétricos: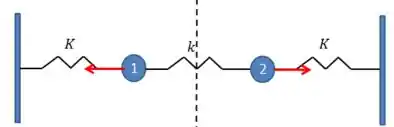
E o assimétrico, deslocamentos assimétricos:
Passo 6
Queremos saber a variação do modo antissimétrico em relação ao modo simétrico. Quer dizer que queremos calcular:
Assim:
Beleza? Como , , assim, podemos usar a aproximação:
Usando:
Vamos ter:
Substituindo em