Dado um sistema de duas partículas de massa ligados por três molas de constante elástica e massa desprezível, como ilustrado abaixo:
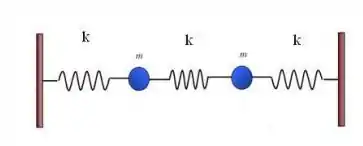
O sistema possui dois modos normais de vibração, e , onde . Quando o sistema oscila com frequência ou , a frequência de oscilação do centro de massa é respectivamente
- e
- e
- e
- e
- e
Passo 1
Nessa questão, as frequências dos modos de vibração já foram dadas. Assim, você não precisa seguir todos aqueles passos pra encontra-las. Porém, o que o enunciado te pede é a frequência de vibração do centro de massa em cada caso.
Bom, pelo arranjo das massas, não podemos esperar muitas formas de movimentação delas.
No primeiro caso, em que o sistema vibra no primeiro harmônico, temos a seguinte configuração:
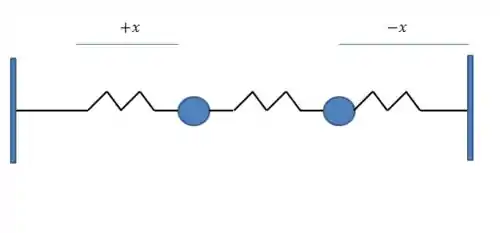
Isso para . Nesse caso, quando uma mola for comprimida por metros, a outra vai ser distendida por metros.
Porém, como o módulo de é o mesmo, já que as massas são as mesmas, a mola central não sofrerá nenhuma alteração:
Ou seja, enquanto uma mola é comprimida metros da esquerda para a direita, a outra é estendida em metros da esquerda para a direita. Isso não gera folgas e, portanto, a mola central não tem seu comprimento alterado.
Então ela se comportar como se fosse uma massa qualquer e vai oscilar com a mesma frequência que as molas: .:
Passo 2
No segundo caso, o esquema fica assim:
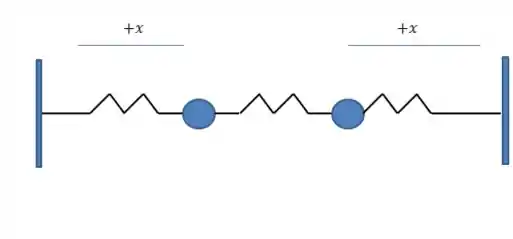
Nesse caso, enquanto uma mola for comprimida, a outra também será comprimida. Enquanto uma for esticada, a outra também será esticada. Isso fará com que a mola do centro sofra alterações no seu comprimento.
Só que tem uma coisa: Estamos analisando o centro de massa, certo?
Pense então: Como as molas são iguais, o que uma sofrer de compressão a outra também sofrerá. Como as forças geradas serão iguais, o centro de massa da mola central não mudará de posição.
Isso pode ser visto calculando-se a somatória das forças sobre o centro de massa:
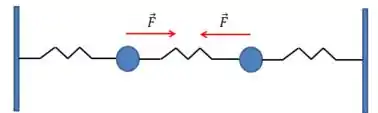
Por que as forças têm sentidos contrários. Assim, como o centro de massa não sofre nenhuma força resultante, a sua posição não muda e não oscila:
Resposta
e)