Considere um sistema formado por duas partículas idênticas de massa ligadas por uma mola de massa desprezível e constante elástica . Supondo que as partículas se movem em apenas uma direção e a única força atuante no sistema advém da mola, assinale a alternativa correta para a frequência angular de oscilação.
Passo 1
Bom, nessa questão temos um caso de uma oscilação acoplada usando apenas uma mola. Além disso, nas extremidades da mola temos massas iguais.
Qual a primeira conclusão que podemos tirar disso? Simetria! Já que temos uma mola e duas massas iguais, podemos esperar que o que gera o movimento de uma massa gera o da outra.
Assim, podemos esperar deslocamentos iguais das massas:
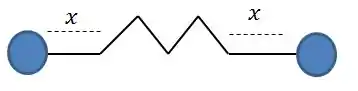
Passo 2
Além disso, quais deverão ser os sentidos dos deslocamentos? Os deslocamentos não podem ter o mesmo sentido.
Qual o motivo disso? Porque o centro de massa precisa ter aceleração nula, logo, o somatório de forças agindo nele deve ser nulo. Isso ocorre porque não temos nenhuma força externa atuando no sistema. Assim, devemos esperar o seguinte sistema de forças:
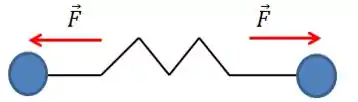
Ou:
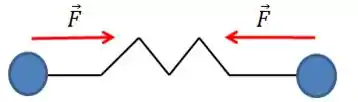
Pra que isso ocorra, quando uma massinha andar a outra deve andar , no sentido contrário. Os deslocamentos são os mesmos em módulo para que as forças sejam iguais. Temos um caso simétrico.
Passo 3
Mas pera ai, se uma massinha anda pra um lado e pro outro, qual a distorção total da mola?
Bom, vai ser a soma dos módulos desses deslocamentos, ou:
Assim, podemos dizer que a força elástica que age em cada massinha é do tipo:
Passo 4
Beleza, então podemos dizer que, pra cada massinha:
Como as duas equações são iguais, não precisamos montar um sistema de EDO’s, calcular determinante, resolver a equação biquadrada, etc. Basta que a gente resolva uma delas, pois vai valer para as duas massas:
Lembrando da definição de frequência:
Pronto!
Resposta
d)