Considere um pêndulo simples formado por uma pequena esfera de massa presa a um fio ideal de comprimento , que é abandonado da posição horizontal. Desconsiderando a resistência do ar é correto afirmar sobre o movimento do pêndulo que:
(a) A força resultante sobre a esfera não tem módulo constante.
(b) A força resultante que atua sobre a esfera aponta sempre na direção do fio.
(c) A esfera descreve um movimento circular uniforme.
(d) Quando a esfera passa pela posição de menor altura, o módulo da tração é igual ao do peso.
(e) A força peso que atua sobre a esfera varia ao longo de sua trajetória.
(f) A força resultante que atua sobre a esfera aponta sempre na direção tangente à trajetória.
Passo 1
Num pêndulo simples, temos duas forças atuando, a força peso e a força de tração :
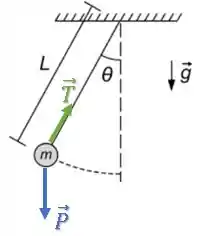
Vamos analisar as opções, começando pela (b).
Passo 2
(b) A força resultante que atua sobre a esfera aponta sempre na direção do fio.
Se decompormos a força peso , podemos ver que existe uma componente da força que está na direção perpendicular à direção do fio (radial), ou seja, a afirmativa é falsa:
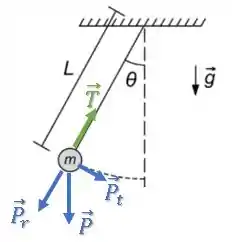
Passo 3
(c) A esfera descreve um movimento circular uniforme.
Ainda com a mesma imagem do item anterior:
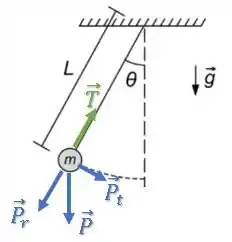
Podemos ver que existe uma componente tangencial da força peso , ou seja, existirá uma aceleração tangencial e por isso não pode ser um movimento circular uniforme.
Passo 4
(d) Quando a esfera passa pela posição de menor altura, o módulo da tração é igual ao do peso.
No momento de menor altura do movimento, temos as duas forças atuando na vertical:

Porém, como o movimento é circular, deve haver uma componente de força radial atuando como centrípeta, ou seja, para que a resultante dessas forças dê uma força apontando para o centro:
Logo, elas não podem ser iguais.
Passo 5
(e) A força peso que atua sobre a esfera varia ao longo de sua trajetória.
A força peso nunca vai variar.
Ela sempre será dada por um vetor apontando verticalmente para baixo e de módulo:
Passo 6
(f) A força resultante que atua sobre a esfera aponta sempre na direção tangente à trajetória.
Não, acabamos de ver um contra-exemplo:

A força resultante nesse caso aponta radialmente para o centro e não tangencialmente ao movimento.
Sempre que o pêndulo estiver realizando o movimento circular com uma certa velocidade, vai existir alguma componente de força atuando como centrípeta e apontando na direção radial.
Passo 7
(a) A força resultante sobre a esfera não tem módulo constante.
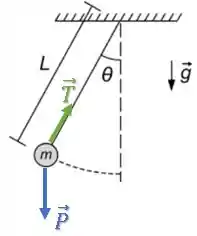
Finalmente, temos que a alternativa (a) está correta.
Primeiro que o módulo da tração vai variar conforme a velocidade do pêndulo varia (resultante centrípeta).
Segundo, que a direção da força de tração vai variar conforme a direção do cabo se altera com relação à partícula, portanto a soma vetorial das duas forças não resultará sempre em uma força com módulo constante.
Resposta
Letra (a)