Questão 2) Um pêndulo é afastado da vertical de um ângulo e solto a partir do repouso. Para que ângulo com a vertical sua velocidade será metade da velocidade máxima atingida pelo pêndulo?
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

Nessa questão, temos um pendulo que inicialmente está a um ângulo com a vertical do seu eixo de rotação.
O pendulo é solto e passa por um ângulo onde nesse momento a sua velocidade é a metade da velocidade máxima que o pendulo atinge.
Que engulo é esse? 🤔
Tem ideia do que fazer?? 🤔🤔
No ponto mais alto do pendulo, sua extremidade não possui velocidade, então sua energia é puramente potencial gravitacional.
Quando o pendulo é solto essa energia é convertida em energia cinética e no menor ponto da trajetória sua extremidade está na velocidade máxima.
A partir daqui podemos pensar no nosso problema!
Bora? 😁
Passo 2
Primeiro vamos imaginar como é a situação inicial do problema
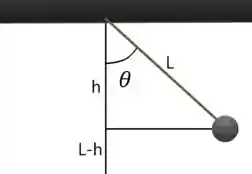
Se o ponto mais baixo que a bola atinge é quando e . No ponto mais alto, podemos dizer que é nossa altura. Mas o que é ?
Como , e a distância horizontal da bola até o eixo central vertical formam um triangulo retângulo, podemos afirmar que é dado por
obs: se o cosseno de um ângulo é o cateto adjacente sobre a hipotenusa, então .
A energia potencial gravitacional é dada por
é a massa da bola, é a aceleração gravitacional e acabamos de calcular.
Fazendo as substituições
Tranquilo até aqui? 👀
Passo 3
Já no ponto mais baixo, quando não temos mais energia potencial e toda a energia foi convertida em energia cinética, temos
Se em a velocidade da bola é a metade da velocidade máxima, vamos ter uma situação de
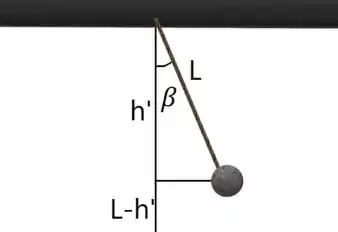
Nesse ponto a bola possui energia cinética, já que parte da energia potencial foi convertida e ainda possui energia potencial já que ela ainda não chegou no ponto mínimo da altura.
Se no ponto máximo é dado por , nesse ponto agora é dado por
E se a energia cinética no ponto mínimo é dada por , a energia cinética nesse ponto, visto que a velocidade é a metade da velocidade , será
Pela lei de conservação de energia, vemos que a energia inicial é igual a energia final, ou seja
Fazendo as substituições, vamos obter
Simplificando a equação cortando dos dois lados, temos
Interessante, não é?
Passo 4
Isolando em um lado da igualdade...
Lembra que ? E que pelo princípio da conservação de energia ? Então
Isolando em um lado da igualdade e simplificando , temos
Substituindo em
Simplificando a equação
Com isso, vemos que o ângulo é o ângulo cujo seu cosseno é igual a do cosseno de !
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
