Um pêndulo é constituído por uma pequena esfera de massa e um fio ideal de comprimento . No instante em que o fio faz um ângulo com a vertical, a resultante das forças que atuam sobre a esfera tem direção horizontal, conforme a figura abaixo. Responda as perguntas abaixo.
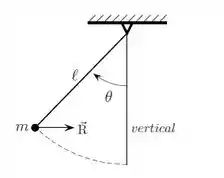
a) Qual o módulo da velocidade da esfera no instante indicado na figura?
b) Supondo conhecido o valor de , qual o módulo da velocidade da esfera quando o fio estiver alinhado verticalmente?
Passo 1
Vamos analisar as forças atuando na partícula:
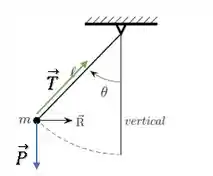
Temos a força peso e a força de tração.
O enunciado nos diz que nesse instante, a força resultante () na partícula é horizontal. Então, vamos decompor as forças nos eixos vertical e horizontal para entender melhor isso.
A força peso já está na vertical, então, vamos decompor a força de tração ():
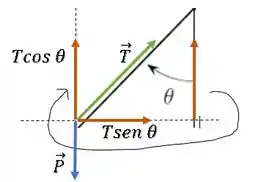
Se a nossa força resultante total () está na horizontal, temos que as forças na vertical têm que se anular. Então com isso tiramos a primeira relação do nosso problema:
Vamos dar uma olhada no primeiro item.
Passo 2
a) Qual o módulo da velocidade da esfera no instante indicado na figura?
Como a partícula no pêndulo percorre uma trajetória circular, podemos pensar numa força centrípeta para achar uma relação entre as forças e a velocidade.
Para isso, vamos decompor as forças, agora, na direção radial (eixo apontando para o centro):
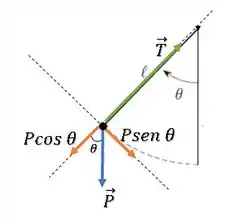
A componente da força resultante que atua como centrípeta será igual ao somatório das forças sobre o eixo passando pelo centro do círculo, ou seja, e a componente da força peso ():
Podemos substituir o valor da força de tração já encontrada ():
Podemos cortar a massa:
Calculando a raiz disso, já encontramos uma expressão para , porém podemos tentar deixar a resposta com uma cara mais amigável:
Com a relação fundamental trigonométrica, temos que ():
Passo 3
b) Supondo conhecido o valor de , qual o módulo da velocidade da esfera quando o fio estiver alinhado verticalmente?
Para resolver esse item podemos pensar na conservação da energia mecânica. Vamos ter a energia potencial gravitacional sendo transformada em energia cinética.
Só para deixar claro, que a energia só se conserva pois a força de tração no fio é sempre perpendicular ao movimento da partícula, logo seu trabalho é zero. Assim, a única força externa que atua na partícula é a força peso, que é uma força conservativa.
Vamos usar o ponto mais baixo como referencial de energia potencial nula.
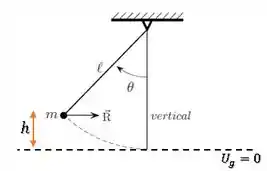
No ponto inicial, a partícula vai ter uma energia cinética () associada à sua velocidade e uma energia potencial gravitacional () associada à sua altura . Já no ponto final, quando o fio estiver na vertical, a partícula vai ter apenas uma energia cinética ():
Conservando a energia mecânica, temos:
Podemos cortar a massa e multiplicar por todos os termos:
Mas como encontramos a altura ?
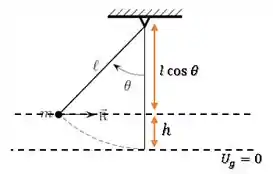
Podemos dizer que:
Voltando à nossa equação, conseguimos encontrar :
Resposta
(a)
(b)