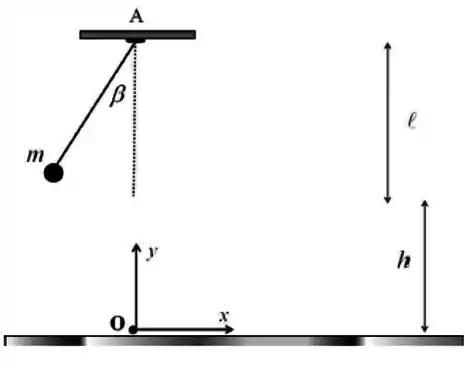
Uma partícula de massa está presa a um fio ideal de comprimento cuja outra extremidade está fixada a um ponto A no teto.

A partícula é largada do repouso quando o fio faz um ângulo com a vertical. Ao passar pelo ponto mais baixo de sua trajetória, o fio se rompe. Utilize o sistema de coordenadas indicado na figura e despreze todas as resistências.

a) Faça um diagrama das forças que atuam sobre a partícula no momento imediatamente anterior ao rompimento do fio.

b) Calcule o vetor velocidade da partícula neste momento, justificando seus cálculos.

c) Calcule o módulo da tensão no fio no instante imediatamente anterior ao seu rompimento.

d) Sendo a altura que a partícula se encontra no momento do rompimento do fio, medida a partir do chão, obtenha a distância horizontal percorrida por ele desde o instante do rompimento do fio até o instante em que ele atinge o chão.

b)

Queremos a velocidade da partícula logo antes do fio romper, sendo que ela partiu do repouso. Então parece uma boa aplicar a conservação da energia mecânica.

Vejamos, a força peso é conservativa. E a força de tensão é sempre perpendicular ao movimento da partícula, então ela não realiza trabalho. Ou seja, não tem nenhuma força não-conservativa realizando trabalho.

Beleza, podemos aplicar a conservação da energia mecânica! A energia mecânica inicial é igual à energia mecânica final :

Sendo a energia cinética e a energia potencial gravitacional, a equação fica:

A partícula sai do repouso, então .

A energia potencial gravitacional é relativa, então vamos considerar que vai facilitar bastante as nossas contas. Ou seja:

sendo a altura inicial da partícula.

Então só precisamos da altura . Pra isso vamos ter que aplicar uma trigonometriazinha. Dá uma olhada nessa figura:

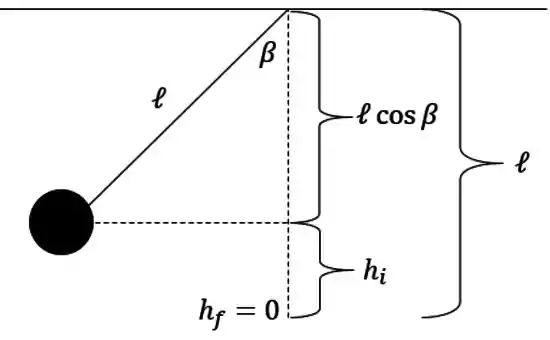
Podemos ver que

Show! Então o módulo da velocidade final que a gente queria é:

Mas ele pediu o vetor velocidade, então temos que ver pra onde ele aponta.

Até logo antes do fio se romper, a partícula está seguindo um movimento circular, então o vetor velocidade é tangente à trajetória. O fio, quando se rompe, está na vertical, então o vetor velocidade está na horizontal, apontando pra direita:

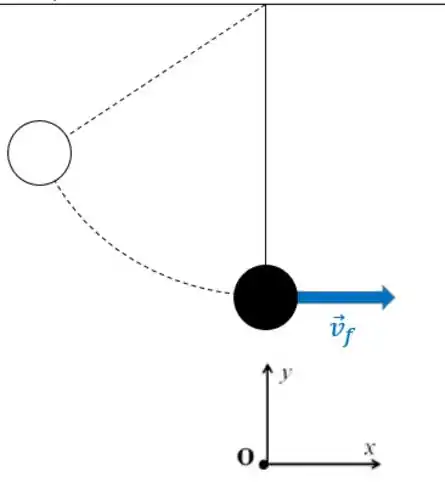
Sendo o vetor unitário do eixo , o vetor velocidade vai ser:

c)

A força resultante atuando na partícula logo antes do fio se romper é:

E pela 2ª lei de Newton,

Logo,

Como a força de tensão aponta pra cima, no sentido do eixo , e a força peso pra baixo, em módulo isso dá:

E essa aceleração a gente consegue achar!

Que nem eu falei antes, logo antes do fio se romper a partícula está seguindo um movimento circular. Na parte mais baixa da trajetória, que é onde o fio se rompe, a sua aceleração é puramente centrípeta!

E a aceleração centrípeta é:

A velocidade a gente já calculou, é , e o raio seria o comprimento do fio , ou seja:

Voltando ao que achamos antes:

d)

Quando o fio se rompe, a tração some então a força resultante sobre a partícula é a força peso:

Então, pela 2ª lei de Newton, vamos ter

Agora a partícula está em queda livre! Mas ela não deixa de ter um movimento horizontal, devido à velocidade que ela tinha quando o fio se rompeu, beleza?

Então o que queremos achar é o alcance da partícula, sabendo que ela foi lançado de uma altura com uma velocidade , e somente sob ação da gravidade.

Vamos separar o movimento em uma componente horizontal e uma vertical, ok?

Começando pela componente horizontal:

A gravidade só age no eixo , no eixo não tem nenhuma força agindo! Ou seja, no eixo a partícula segue um MRU com velocidade .

Então no eixo as equações do movimento são:

Agora vamos ver a componente vertical.

Como já vimos, na vertical o movimento é de queda livre, um MRUV com aceleração . A velocidade da partícula quando o fio se rompe é somente horizontal, no eixo ela é nula.

Então no eixo as equações do movimento são:

Quando a partícula chega no chão, seu deslocamento vertical é nulo. Então digamos que é o tempo no qual a partícula toca o chão. Isso significa que:

No tempo o deslocamento horizontal da partícula é justamente o alcance que queremos achar. Vamos chamar esse alcance de . Então temos