Foi feito um experimento com um pêndulo simples, consistindo de uma massa , presa na extremidade de um fio ideal, que tem sua outra extremidade presa ao teto. Foi construído a partir desse experimento um gráfico da energia cinética, , em função do tempo , mostrado abaixo.
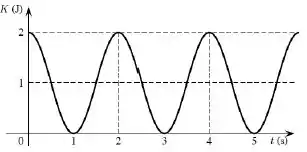
Considere a aceleração da gravidade como sendo . Qual a variação na altura do pêndulo durante o movimento?
(a)
(b)
(c)
(d)
(e)
(f)
Passo 1
Temos um gráfico da energia cinética e queremos uma informação relacionada com a altura.
O que essas coisas têm a ver?
Bom, a energia potencial gravitacional depende da variação de altura:
Beleza, mas como relacionamos a energia cinética com a potencial gravitacional?
Dá uma olhadinha nas forças atuando sobre o pêndulo:
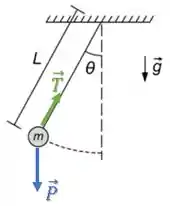
Mas e daí?
Então, a força de tração ela está sempre perpendicular ao movimento do pêndulo, ou seja, por mais que ela seja uma força não conservativa, ela não realiza trabalho e portanto não retira energia do sistema.
Já a força peso é uma força conservativa mesmo, então ela também não retira energia do sistema.
Com isso, chegamos à conclusão de que a energia mecânica do sistema se conserva... tchanam!
Ou seja, a energia mecânica sempre vai ter o mesmo valor e fica variando entre a forma de potencial gravitacional e cinética :
Passo 2
Como a energia oscila de forma, porém a energia total se mantém, podemos considerar que quando a energia cinética é máxima, a potencial é mínima e vice versa.
Então a variação da energia potencial gravitacional vai ser a mesma variação da energia cinética:
Olhando para o gráfico, podemos ver que a variação é de:
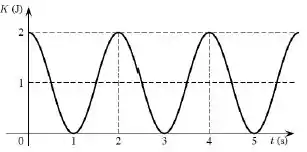
Substituindo os valores:
Ou seja:
Resposta
Letra (a)