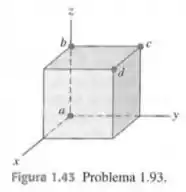
Um cubo é colocado de um modo que um dos vértices esteja na origem e três arestas coincidam com os eixos de um sistema de coordenadas (Figura ). Use vetores para calcular:
- O ângulo entre a aresta ao longo do eixo (linha ) e a diagonal da origem até o vértice oposto (linha );
- O ângulo entre a linha (a diagonal de uma das faces) e a linha .
Passo 1
Como queremos saber o ângulo entre os vetores, vamos usar o produto escalar, pode ser?
Passo 2
Vamos escrever o vetor que representa cada segmento que foi dado no problema:
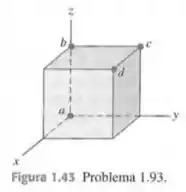
Passo 3
Alternativa a)
Fazendo o produto escalar entre as linhas e
Isolando o temos:
Logo:
Passo 4
Alternativa b)
Fazendo o produto escalar entre as linhas e
Isolando o temos:
Logo:
Resposta
Exercícios de Livros Relacionados
Verdadeiro ou falso: (a) O produto escalar não pode ter unidades. (b) Se o produto escalar de dois vetores diferentes de zero for zero, eles serão paralelos. (c) Se o produto escalar de dois vetores d
Para quaisquer dois vetores A → e B → , mostre que A → ∙ B → = A x B x + A y B y + A z B z . Sugestões: Escreva A → e B → na forma de vetor unitário e use as Equações 6.4 e 6.5.
Dois vetores a → e b → têm componentes, em metros, a x = 3,2 , a y = 1,6 , b x = 0,50 e b y = 4,5 (a) Determine o ângulo entre a → e b → . Existem dois vetores no plano x y que são
O módulo do vetor A é 6,00 unidades, o módulo do vetor B é 7,00 unidades e A · B=14,0 . Qual é o ângulo entre AeB ?
Use a definição de produto escalar , a → . b → = a . b . cos ∅ e o fato de que a → . b → = a x b x +a y b y + a z b z para calcular o ângulo entre os vetores a → =3,0 i →+3,0 j →+3,0 k → e b →=2,0 i