UFABC – Fundamentos de Mecânica – Lista 1 – Questão 7
Um tubo de água desce pela parede sul de um prédio fazendo um ângulo de com a horizontal,
ao chegar na parede oeste o tubo continua por ela fazendo igual um ângulo de com a horizontal.
Qual é o ângulo que faz a tubo da parede sul com o tubo da parede oeste?
Passo 1
Oi, tudo bem? Essa questão parece complicada, mas vou ajudar você! Temos dois canos, um descendo por uma parede sul (ou seja, na face do fundo de um cubo) fazendo um ângulo de com a horizontal. Depois que esse cano chega na parede oeste (ou seja, a parede do lado esquerdo), ele desce sob um ângulo de ainda com a horizontal.
e o problema pede para calcular o ângulo entre esses canos!
A ideia aqui é colocar em termos de vetores unitários esses dois canos! E calcular o ângulo entre esses dois vetores através do produto escalar:
Mas calma, vou fazer passo a passo contigo!
Passo 2
Primeiro vamos construir esses dois vetores!
Primeiro o da parede sul:
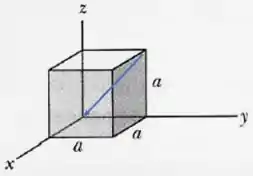
Ele faz um ângulo de com a horizontal. Como a parede sul está na posição , a componente desse vetor é zero. As outras duas componentes somadas ao quadrado devem ser 1, e devem ser negativas, pois o cano desce em direção à parede da esquerda. Assim esse vetor é:
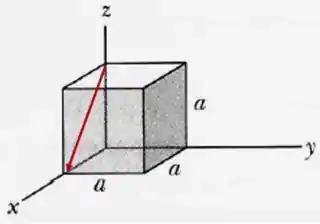
Agora a componente que é zero é a do y. As outras componentes seguem sendo negativas, pois esse cano também desce. Assim esse outro vetor é:
Beleza?
Passo 3
Como são vetores unitários , aí o produto escalar fica mais fácil:
Nosso próximo passo é calcular esse produto escalar . É só multiplicar componente a componente e somar o resultado:
Mas qual será o ângulo que buscamos? vamos colocar um vetor na sequência do outro no desenho e aí você vai poder ver que o ângulo correto é o de :
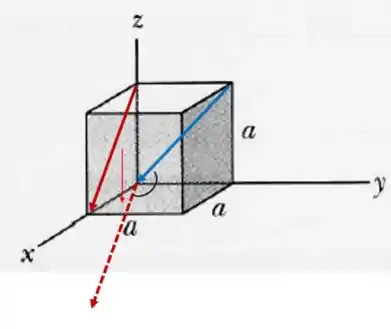
E é isso!
Espero ter ajudado!