Em um movimento circular uniforme onde os vetores posição, velocidade e aceleração da partícula valem , e , respectivamente, (considere a origem do sistema de referência no centro do círculo) marque a alternativa correta para o resultado das seguintes equações: , e :
(A) 1, 0, 0, respectivamente
(B) 0, 0, 0, respectivamente
(C) 0, 1, 0, respectivamente
(D) 0, -1, 0, respectivamente
(E) -1, 0, 0, respectivamente
Passo 1
Para fazer essa questão, vamos lembrar duas coisas.
A primeira é como funcionam esses vetores no movimento circular uniforme.
O vetor posição vai do centro do círculo até a partícula:
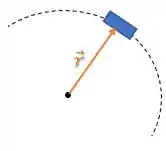
A aceleração sobre o corpo atua como uma aceleração centrípeta apontando para o centro da curva:
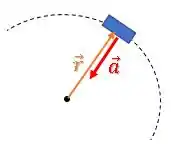
E o vetor velocidade é sempre tangente à curva:
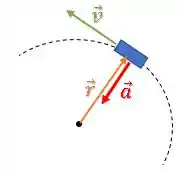
Vamos relembrar agora o produto escalar.
O produto escalar entre dois vetores resulta em um número e nós calculamos com:
Sendo o ângulo entre eles.
Passo 2
Show, então vamos aplicar esse conceito em cada um dos casos.
Primeiro:

O ângulo entre e é .
Eles estão na mesma direção mas em sentidos contrários:

Segundo:
Pegou o espírito né?
Basta calcularmos o cosseno do ângulo entre os vetores.

Os vetores e são perpendiculares, logo :
Terceiro:

Os vetores e também são perpendiculares:
Então, ficamos com -1, 0, 0, respectivamente (letra E).
Resposta
Letra (E)