O gráfico abaixo representa a emitância espectral (distribuição de intensidade) de um corpo negro como função do comprimento de onda.
É dada apenas a escala do eixo de comprimento de onda em . Faltou colocar no gráfico a unidade da escala do eixo da distribuição de intensidade.
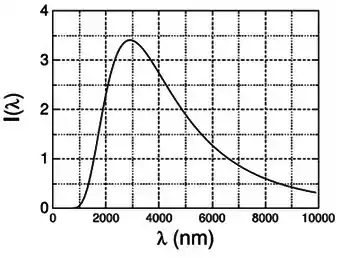
- Calcule a intensidade total irradiada por esse corpo.
- Calcule aproximadamente a intensidade irradiada na faixa de comprimentos de onda entre e .
- Caso a temperatura do corpo seja dobrada. Determine o comprimento de onda do máximo da nova curva e a intensidade total irradiada.
Passo 1
Letra a)
Para sabermos a intensidade total irradiada por esse corpo, primeiro precisamos de sua temperatura.
Podemos usar para isso a lei de Wien, que relaciona o comprimento de onda de máxima emitância espectral com a temperatura.
Pelo gráfico, . A temperatura será:
Passo 2
De posse da temperatura, usamos a lei de Stefan Boltzmann.
Onde
Como vimos antes, . Substituindo tudo:
Passo 3
Letra b)
Neste caso, teremos que abrir mão de uma aproximação meio forçada.
A intensidade entre e vai ser a área embaixo dessa parte da curva.
A integral da equação que nos dá a curva do espectro de corpo negro é muito complicada, e é inviável tentarmos utilizá-la.
Mas como a intensidade total é a área sob a curva, então vamos tentar contar o número de quadrados sobre a curva, e utilizá-los como unidade de medida para encontrar a razão entre essa intensidade e a intensidade total.
Como isso é pouco objetivo (qual critério usar para contar quadrados cortados pela curva, que parte da área está debaixo da curva e parte acima), podemos encontrar diferentes valores.
Passo 4
De forma geral, podemos aceitar que tem entre 3 e 4 quadrados abaixo da faixa de a . Vou usar quatro.
Para contar o resto da curva, é bem complicado, mas vou considerar o seguinte:
Entre , temos aproximadamente 2 quadrados (um pouco menos, mas arrendondei pra cima para consertar o da faixa seguinte).
Entre e , temos aproximadamente 12 quadrados (um pouco mais, mas arrendondei para baixo por causa da faixa anterior).
Entre e , temos aproximadamente 8 quadrados (tá mais pra 7, mas vamos errar pra mais essa área total).
Entre e , temos 4 quadrados (de novo, é mais próximo de 3, mas vamos na margem de erro).
Entre e o fim da curva, temos uns 2 quadrados.
Assim, o total de quadrados é , e a razão entre a intensidade procurada e a intensidade total vai ser:
Passo 5
Letra c)
A lei de Wien nos diz que:
Logo, se dobrarmos a temperatura, o novo comprimento de onda vai ser metade do anterior:
Já a lei de Stefan Boltzmann nos diz que:
Se dobrarmos a temperatura, a nova intensidade será:
Resposta
Letra a)
Letra b)
Letra c)