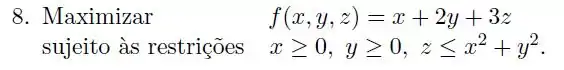
Passo 1
Vamos ver se todas as condições do teorema de Weierstrass são satisfeitas:
Começamos verificando a continuidade da função
É uma função polinomial, então é contínua em todo .
Passo 2
Vamos verificar se o conjunto dado é fechado. Perceba que:
A equação significa que nosso conjunto é um paraboloide e seu interior ao longo do eixo .
As equações são planos que fecham dois lados do nosso paraboloide no eixo e no eixo .
Desse modo, o paraboloide é fechado por “3 lados”, mas como não temos nenhuma outra restrição para fechá-lo no eixo (como se fosse uma tampa pro pedaço do paraboloide que temos), nosso conjunto não é fechado.
Assim, podemos parar por aqui e dizer que o problema não tem solução, já que nem todas as condições do teorema foram satisfeitas.
Resposta
Não
Exercícios de Livros Relacionados
Determinar o ponto P(x, y, z) do plano x +3 y +2 z =6 , cuja distância à origem seja mínima.
Determine, pelo método dos mínimos quadrados, a reta que melhor se ajusta aos dados:(1, 2), (0, 0) e (2, 3).
Determine, pelo método dos mínimos quadrados, a reta que melhor se ajusta aos dados:(0,1), (1, 2), (2, 3) e (2, 4).
Uma firma de embalagem necessita fabricar caixas retangulares de 64 cm³ de volume. Se o material da parte lateral custa a metade do material a ser usado para a tampa e para o fundo da caixa, determina
Determinar três números positivos cujo produto seja 100 e cuja soma seja mínima.