Considere a função dada por
Onde é o domínio .
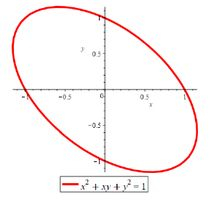
- Encontre e classifique os pontos críticos de no interior do domínio .
- Explique por que os valores extremos absolutos de devem existir em .
- Encontre os valores máximos absolutos e mínimos absolutos de em . Indique os pontos de onde esses valores extremos são atingidos
Passo 1
Fala povo, tudo certo? Galera, pra começo de conversa, vamos lembrar que pontos críticos são aqueles que zeram a nossa derivada. Nesse caso, como a função tem duas variáveis, os pontos críticos zeram as nossas derivadas, no plural:
Bora derivar então? Pra começar, pegamos e usamos a regra da cadeia:
E ó só galera, até então a gente não derivou nada especificamente em relação a . Portanto, pra , até agora, a ideia é a mesma:
E derivando quem sobrou nos dois casos, temos:
Portanto, queremos achar o conjunto de pontos que satisfaça:
E veja só! A única forma disso ser possível é se:
Afinal, pra essas equações zerarem, o denominador acaba não influenciando em nada. O único ponto crítico de vai ser então que, se olharmos com cuidado o enunciado, vemos que ele está dentro do domínio da função:
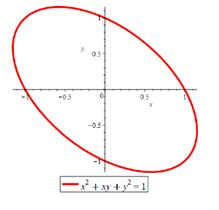
Passo 2
Agora bora classificar esse ponto crítico. Pra isso vamos ter que fazer teste da segunda derivada e montar uma matriz Hessiana, lembrando que:

Bora ver essas derivadas então! Seja:
Encontramos:
E pela regra do quociente:
No ponto , vai assumir o seguinte valor:
Agora, seja a outra derivada:
Encontramos ao derivar e mantendo a ideia de usar regra do quociente:
Aplicando o ponto :
Show, temos a primeira linha da Matriz Hessiana no ponto , que será:
Passo 3
Bora pra segunda linha da matriz Hessiana. Ela começa querendo encontrar:
Onde:
Agora pondo a mão na massa e calculando mais essa derivada, temos:
Aplicando o ponto , achamos:
Ufa, quase lá! Falta só uma derivada, que será:
Usando a regra do quociente:
No ponto , vai assumir o seguinte valor:
A matriz então finalmente fica pronta:
De forma que . Como também, concluímos lá pela imagem do Passo que temos um ponto de mínimo local. Ufa! Letra fechada!
Passo 4
Próxima letra! Essa é mais teórica. A gente tem quer provar que existem extremos absolutos dentro da região ? Mas como? Oras, pedindo ajuda pro Teorema dos Valores Extremos, se:
- é contínua
- O domínio é fechado
- O domínio é limitado
Então com certeza existem extremos absolutos dentro de . A primeira condição a gente já tem na mão. Afinal, logaritmos são funções que são sempre contínuas, ok? Agora, olhando com calma pro :
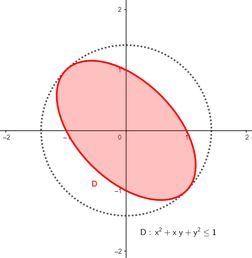
Bem, se o domínio contém sua própria fronteira, então ele é de fato fechado. E como a gente consegue estabelecer um círculo imaginário que contém o domínio na sua totalidade, além de fechado ele é limitado! Tai provado! Existem sim extremos absolutos pra dentro de .
Passo 5
Última letra agora galera! Na letra achamos todos os pontos críticos que existem dentro de . Mas e na sua fronteira? É exatamente isso que veremos agora! Pra isso, bora usar Multiplicadores de Lagrange com uma restrição, ok? A restrição que vamos usar nada mais é do que a equação da elipse que definde :
Sendo assim, vamos ter:
O que é o mesmo que o seguinte sistema:
Do qual as primeiras derivadas, pra , já conhecemos:
Falta fazer as derivadas parciais de :
Chegamos a:
Po galera, é só uma constante! Podemos eliminar ela de boas ao igualarmos as duas definições acima:
E aplicando a distributiva:
Opa, algo que da pra trabalhar em! A gente vai achar os pontos que queremos na fronteira de se considerarmos essa igualdade dentro da restrição. Primeiro, pra , temos:
O que resulta em dois pontos pra gente, já que :
Agora, pro outro caso, onde , vamos ter:
Ai dessa vez, por estarmos usando , a gente intercala os sinais nos pontos possíveis:
Passo 6
Galera, promeeeeto que é o último passo! No anterior achamos os pontos, mas não sabemos o valor da função neles:
Tudo que vamos fazer agora é calcular exatamente isso pra
Bora lá então? Vamos ter:
Considerando que ainda tínhamos o ponto crítico pra considerar, ficamos ainda com:
É galera, 5 pontos, mas só três valores de considerando todos esses pontos:
Como é uma função crescente, nem precisamos de calculadora pra organizar esses números. Quanto maior o interior, maior o valor do logarítimo, de forma que:
Sendo assim, o máximo absoluto é obtido quando é alcançado, isto é, nos pontos e . Já o mínimo absoluto é alcançado quando é o resultado do valor da função, o que ocorre no ponto . Ufa, cabou!
Resposta
- Um único ponto crítico , classificado como ponto de mínimo
- Pelo Teorema do Valor Máximo, as três condições a seguir, que são satisfeitas no nosso problema, são o suficiente pra provar que existem extremos absolutos dentro de : é contínua; o domínio é fechado; o domínio é limitado.
- O máximo absoluto é obtido quando é alcançado, isto é, nos pontos e . Já o mínimo absoluto é alcançado quando é o resultado do valor da função, o que ocorre no ponto