Um observador na Terra (referencial ) observa duas naves espaciais e movendo-se com a mesma velocidade , constante, separadas por uma distância igual a . Este mesmo observador vê no instante a proa da nave , com coordenada , emitir um pulso de luz e no instante a popa da nave emitir um outro pulso de luz, conforme a figura. O referencial da Terra e o referencial ’no qual as naves estão em repouso coincidem em .
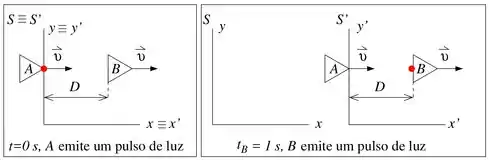
(a) Calcule no referencial a coordenada do pulso emitido pela nave no instante .
(b) Calcule no referencial o instante em que o pulso é emitido pela nave .
(c) O pulso de luz emitido por poderia ser uma resposta ao pulso de luz emitido por ?
(d) Calcule a distância entre as naves no referencial .
Passo 1
No referencial a distância da nave à origem de no tempo (medido em ) será a distância mais o quanto a nave percorreu nesse intervalo de tempo a velocidade de . Assim
Passo 2
Sabemos que a emissão do sinal ocorreu em no referencial . Para calcular o tempo de emissão do sinal no referencial temos que fazer uma transformação de Lorentz
Pelo enunciado , e já achamos no item anterior. Assim
Passo 3
O sinal de A foi emitido em (os tempos coincidem em , segundo o enunciado). Para que o sinal de fosse uma resposta ao sinal de ele deveria no seu referencial emitir o sinal depois do sinal de .
Como o sinal de foi antes do sinal de (já que ) então não foi uma resposta a .
Passo 4
Aqui temos uma contração de comprimento. Como o comprimento próprio no referencial é e a velocidade relativa entre os referenciais é , temos
Resposta
- Como o sinal de foi antes do sinal de (já que ) então não foi uma resposta a .