Um veículo se move com velocidade uniforme em relação ao solo. Sejam e as extremidades do veículo e e marcações no solo, como na figura.
Definamos o evento como a passagem de por e os eventos , e de forma análoga.
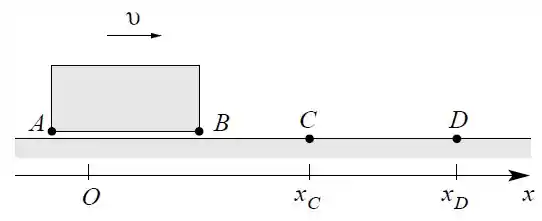
- Se o intervalo de tempo entre os eventos e (tempo gasto pelo veículo para passar pelo ponto ) no referencial do veículo é , qual é o intervalo de tempo entre esses eventos no referencial do solo?
- Se os eventos e são simultâneos no referencial do veículo, qual é o intervalo de tempo entre esses eventos no referencial do solo?
- Qual é a ordem temporal dos eventos e no referencial do solo?
Passo 1
Letra a)
Neste caso, o intervalo de tempo próprio é aquele medido pelo referencial do solo pois, para ele, os dois eventos se deram no mesmo ponto no espaço.
Podemos então usar a fórmula da dilatação do tempo:
Ou seja, o intervalo de tempo no referencial do solo é dado por:
Onde
Se desejar, podemos reescrever a equação sem o
Passo 2
Letra b)
Para achar o intervalo de tempo entre os eventos e no referencial do solo precisamos usar as transformações de Lorentz.
Como os eventos foram simultâneos no veículo, temos:
Sendo é o comprimento entre os pontos e para o veículo, que coincide com seu comprimento próprio (entre e ). Podemos usar a transformação de Lorentz no comprimento para simplificar essa equação:
Substituindo:
E o comprimento é a distância entre os pontos e medida no referencial do solo, que vai ser a distância própria.
Passo 3
Letra c)
No item anterior, vimos que do referencial no solo o tempo entre os eventos e é
Como podemos perceber, pois .
Porém, para saber qual evento ocorreu primeiro, precisamos estar claros em quem é .
Nas transformações de Lorentz anteriores, estávamos sempre usando como variação a diferença do evento para o evento . Por isso:
Então o instante em que ocorreu o evento foi anterior ao instante em que ocorreu o evento .
Resposta
Letra a)
Letra b)
Letra c)
O evento ocorreu antes do evento .