Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Transformações Lineares Geométricas

Ver Teoria
Exercício 2134567891011121314

Enunciado

Determine a matriz que realiza as seguintes transformações no R 2 :

a   Amplia todos os vetores por um fator k

b   Reflete os vetores em torno do eixo X .

c   Projeta os vetores no eixo X .

d   Reflete os vetores em torno da reta Y = X

Passo 1

a Bom, essa matriz representa a T L que faz o seguinte:

T x , y = ( k x , k y )

Aplicando na base canônica do R 2 :

T 1,0 = k , 0

T 0,1 = 0 , k

Logo,

T = k 0 0 k

Passo 2

b Ao refletirmos os vetores em torno do eixo X , nós estamos mantendo as componentes em X inalteradas e multiplicando as componentes em Y por - 1 . Logo:

T x , y = ( x , - y )

Temos então que:

T 1,0 = 1,0

T 0,1 = 0 , - 1

Com isso,

T = 1 0 0 - 1

Passo 3

c   Quando projetamos os vetores no eixo X , estamos mantendo inalteradas as componentes deles em X e zerando as componentes de Y . Portanto:

T x , y = x , 0

Então,

T 1,0 = 1,0

T 0,1 = 0,0

E

T = 1 0 0 0

Passo 4

d   Essa é um pouco mais complicada. Ela Mantém inalteradas as componentes do vetor sobre a reta x = y e multiplica por - 1 as componentes perpendiculares a ela (sobre a reta x = - y ). Olha essa imagem pra te ajudar:

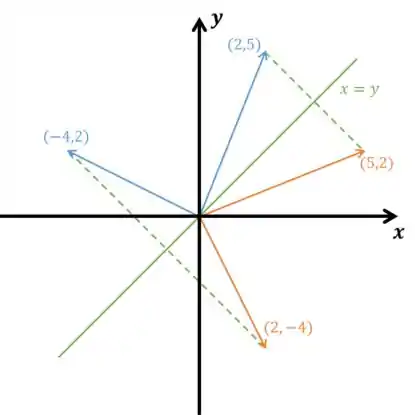
Opa, agora ficou fácil. O que ela faz, no final das contas, é trocas as componentes x e y dos vetores! Logo:

T x , y = y , x

T 1,0 = ( 0,1 )

T 0,1 = 1,0

Então,

T = 0 1 1 0

Resposta

a   k 0 0 k

b   1 0 0 - 1

c   1 0 0 0

d   0 1 1 0

Exercícios de Livros Relacionados

Nos Exercícios 17-20, encontre a solução geral do sistema linear e confirme que os vetores linha da matriz de coeficientes são ortogonais aos vetores solução.20. x 1 + 3 x 2 - 4 x 3 = 0x 1 + 2 x 2 + 3
22.(a) A equação x + y = 1 pode ser vista como um sistema linear de uma equação em duas incógnitas. Expresse uma solução geral dessa equação como uma solução particular somada com uma solução geral do
Nos Exercícios 27-28, encontre uma solução geral do sistema e use essa solução para encontrar uma solução geral do sistema homogêneo associado e uma solução particular do sistema dado. 27. 3 4 1 2 6 8
Nos Exercícios 27-28, encontre uma solução geral do sistema e use essa solução para encontrar uma solução geral do sistema homogêneo associado e uma solução particular do sistema dado. 28. 9 - 35 6 6
Nos Exercícios 13-14, encontre as equações vetoriais e paramétricas da reta em R 2 que passa pela origem e é ortogonal a v .13. v = - 2,3