Considere os planos paralelos
E o ponto .
(a) Determine a projeção ortogonal do ponto P na reta .
(b) Determine a projeção ortogonal do ponto P no plano .
(c) Determine o espelhamento (reflexão) do ponto P em relação ao plano
(d) Considere o ponto Observe que o ponto pertence a e que (ou seja, transladando P pelo vetor obtemos Q). Determine o espelhamento de Q em relação ao plano
Passo 1
(a) Primeiro vamos lembrar como achamos a matriz de projeção ortogonal quando estamos projetando em uma direção v:
Achando essa matriz, se quisermos projetor um vetor na direção , basta fazer o produto da matriz pelo vetor .
Nessa questão, queremos projetar na reta
Que é na verdade a direção do vetor (só colocar o parâmetro t pra fora e ver qual a direção da reta).
Então nossa matriz vai ficar:
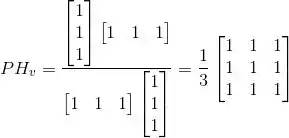
Como a reta r contém a origem, projetar o ponto P é a mesma coisa que projetar o vetor =(1,1,0).
Então vamos fazer:

Passo 2
(b) Note que a direção em que projetamos P anteriormente é a mesma direção do vetor normal do plano .
O que tá acontecendo no espaço é mais ou menos isso aqui:
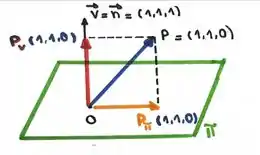
Ou seja, podemos escrever:
Ou seja:
Substituindo:
Passo 3
(c) Quando falamos da reflexão de P em relação ao plano , estamos pensando no seguinte:
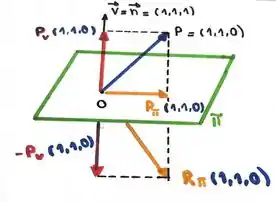
Então temos que:
Mas vimos antes que:
Então:
Substituindo os valores que já achamos:
Passo 4
(d) ) Considerando os pontos e dados.
Temos:
Além disso, os planos dados foram:
Note que o plano pode ser visto como o plano transladado de (1,0,0).
Dessa forma, refletir Q por é a mesma coisa que refletir P por e somar (1,0,0).
Sabemos do item anterior quanto vale a reflexão de P por
Logo:
Resposta
(a)
(b)
(c)
(d)