A figura ao lado mostra um bloco de alumínio de massa 1 kg e um bloco de ferro de massa 2 kg. A temperatura do bloco de alumínio é 300 K enquanto a temperatura do bloco de ferro é 500 K. Os blocos estão em uma caixa isolada termicamente e estão separados por uma divisória isolante. Quando removemos a divisória, depois de algum tempo, os blocos atingem a temperatura de equilíbrio. O calor específico do alumínio é = 900 J/kgK e o calor específico do ferro é = 450 J/kgK.
a) Qual a temperatura de equilíbrio?
b) Sem realizar cálculos, responda: A variação de entropia do sistema “bloco de alumínio + bloco de ferro" é positiva, negativa ou nula? Justifique sua resposta.
c) Qual é a variação de entropia do sistema “bloco de alumínio + bloco de ferro"? (sua resposta pode ficar em termos de frações simplificadas)
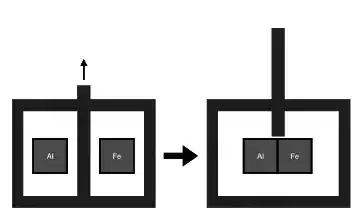
Passo 1
a) Aqui nós vamos usar transferência de calor! O calor recebido por um mais o cedido por outro vai ser zero. Então:
Passo 2
b) É positiva! Pode dizer sem medo!
Mas por quê?
Porque é um processo irreversível! Então a entropia é maior que zero. O processo é irreversível porque, depois de atingido o equilíbrio térmico, os blocos não voltam a trocar calor espontaneamente.

Passo 3
c) A entropia é:
E como o calor é sensível nos dois blocos:
Escrevendo na forma diferencial:
Então:
Show! Vamos calcular pros dois caras.
A variação de entropia no sistema vai ser então:
E como , isso comprova o que dissemos no item B que .
Resposta
a)
b)
c)