1. Um tacho com capacidade térmica desprezível contém de água a . Um cilindro de cobre de , muito quente, é jogado na água, fazendo a água ferver e transformando da água em vapor. O processo ocorre a pressão atmosférica. A temperatura final do sistema é de . Despreze a transferência de calor para o ambiente.
1. Qual é a energia transferida para a água na forma de calor?
2. Qual é a temperatura inicial do cilindro?
3. Calcule a variação de entropia total do sistema durante esse processo.
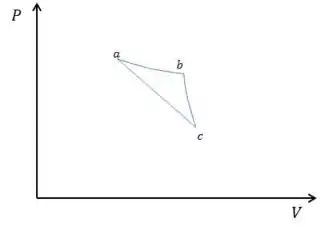
2. No diagrama abaixo, o gás realiza de trabalho quando percorre a isoterma e quando percorre a adiabática . Calcule a variação de energia interna do gás quando percorre a trajetória retilínea

Dados:

b)

Agora podemos voltar à equação:

Bom, o calor perdido é dado apenas pela queda de temperatura do cobre:

Assim:

c)

A variação total de entropia é dada por:

Ai você precisa se ligar que o cobre perde calor, então você deve usar o sinal negativo para o valor do calor perdido, assim com a água ganha calor, então você precisa usar valores positivos de calor.

A variação de entropia é dada por:

Para o caso em que levamos em consideração uma variação sensível de calor, temos:

E no caso em que ocorre uma mudança de fase, como evaporação, a temperatura permanece constante e temos:

Vamos antes passar as temperaturas para Kelvins:

Assim, pro cobre vamos usar a primeira opção:

E pra água:

Assim:

II)

Nós queremos saber

Podemos calcular isso usando o fato de que a a variação total de energia interna de um ciclo é nula. Isso quer dizer que a soma de todas as variações de energia interna é nula:

Bom, quanto vale Como essa transformação é uma isoterma, a variação da energia interna é nula. Assim:

E a variação Essa é uma transformação adiabática, então:

Do enunciado:

Assim: