Considere o plano e os pontos e .

a) Escreva uma equação vetorial da reta definida por e .

b) Escreva a equação geral do plano que contém e e é perpendicular a .

c) Escreva uma equação vetorial da reta que é a projeção ortogonal da reta definida por e no plano .

d) Determine o ângulo entre a reta definida por e e o plano .

b) Primeiramente, se o plano deve ser perpendicular a , ele vai ser paralelo ao vetor normal de , ou seja, paralelo a . Além disso, se esse plano contém os pontos e , ele deve ser paralelo também ao vetor .

Para que um ponto genérico pertença ao plano , o produto misto de , e deve ser 0:

Calculando esse determinante, temos que

Que é a equação do plano :)

c) Bom, a reta é definida pelos pontos que são as projeções de e no plano . Mas ei, observe que o ponto já é pertencente ao plano (pois ) e também é pertencente ao plano , como definimos no passo anterior.

Agora vamos usar uma figura pra pensar melhor:

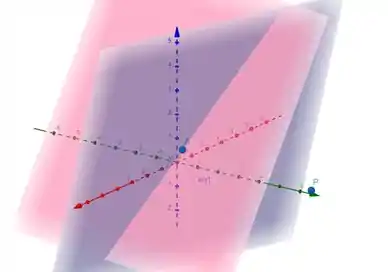
Sabendo que o plano roxo é e o plano rosa é e lembrando que o ponto pertence a também, observe geometricamente que a projeção de no plano vai ser na intersecção de com , que é o mesmo lugar onde está o ponto .

Logo, a reta definida pelas projeções vai ser a intersecção dos planos e , dada pelo sistema:

Multiplicando a equação de baixo por 4 e subtraindo as duas, vamos ter

Então . Substituindo isso na equação de baixo:

Então o vetor diretor dessa reta vai ser dado por

Então a equação vetorial dessa reta vai ser dada por

d) Observe que como a reta está contida no plano (sim, ela ta na intersecção, mas não deixar de estar contida hehe), calcular o ângulo entre e é a mesma coisa que calcular o ângulo entre e o vetor diretor de !! A gente faz isso pela formulazinha do produto escalar:

Logo