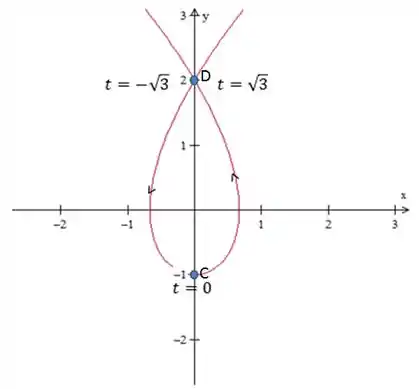
Calcule a área da região do plano limitada pelo laço da curva de equações paramétricas , considerando o seu gráfico a seguir:
Passo 1
Vamos verificar se há trechos repetidos.
Vamos calcular a área limitada pelo laço da curva . Pelo gráfico, é possível perceber que não há trechos repetidos.
Passo 2
Identificar qual dos 3 tipos de cálculo de áreas vamos usar.
Pelo gráfico, notamos que o problema pode ser resolvido se calcularmos a área entre a curva e o eixo .
Passo 3
Substituir as informações na integral para calcular a área.
A fórmula para calcular a área é:
Onde é a curva á esquerda do eixo e é a curva a direita do eixo .
No nosso caso a curva é a mesma, o que vai mudar são os limites de integração.
Curva a esquerda do eixo :
Curva a direita do eixo
Vamos encontrar :
Podemos calcular
Agora vamos calcular os limites de integração.
Vamos analisar a parte da curva a esquerda do eixo . O valor de no ponto é e o valor no ponto é
Analisando a curva a direita, temos:
O valor de no ponto é , e no ponto é
Portanto, a integral fica:
Repare que tem esse menos na primeira integral, pois a curva está a esquerda do eixo Substituindo:
Passo 4
Calcular a integral
Ajeitando:
Calculando temos:
Portanto: