Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Área de Curvas Parametrizadas

Ver Teoria
Exercício 1312345678910111214

Enunciado

USP, Sem Campus, Cálculo 3, lista 3 - 2022.1, Questão 1g

Determine uma representação paramétrica de cada uma das superfícies abaixo e calcule sua área:

g) S é o toro obtido pela rotação da circunferência no plano x z cm centro b , 0,0 e raio a < b em torno do eixo z .

Passo 1

Eaee!!! Belezinha? Bom... a questão nos pede para determinarmos uma representação paramétrica de S em que S é o toro obtido pela rotação da circunferência no plano x z cm centro b , 0,0 e raio a < b em torno do eixo z . Ou seja:

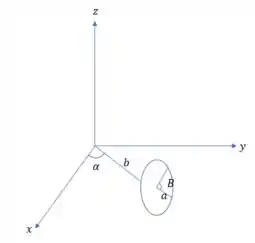
A questão também nos pede para calcular a sua área.

Para podermos resolver isso, primeiramente temos que parametrizar a superfície para a qual estamos trabalhando para prosseguir com os próximos passos que vamos ver juntos, belezinha?

Não entendeu? Então bora junto 😉

Passo 2

Bom... parametrizando, temos:

  • x = b + a cos ⁡ θ ∴

  • z = a   s e n   θ

Fazendo relação com a circunferência, temos:

ϕ α , θ = x cos ⁡ α ,   x   s e n   α , z ∴

ϕ α , θ = b + a cos ⁡ θ cos ⁡ α ,   b + a cos ⁡ θ   s e n   α , a   s e n   θ  

Passo 3

Já para a região D tem-se os intervalos 0 < α < 2 π e 0 < θ < 2 π .

Passo 4

Já para a área A , devemos fazer:

A = ∬ ∂ ϕ ∂ α × ∂ ϕ ∂ θ d α   d θ

Dessa forma, fazemos:

  • ∂ ϕ ∂ α = - b + a cos ⁡ θ cos ⁡ α , b + a cos ⁡ θ cos ⁡ α , 0

  • ∂ ϕ ∂ θ = b + a cos ⁡ θ cos ⁡ α , b + a cos ⁡ θ s e n   α , a   s e n   θ

Portanto, temos:

∂ ϕ ∂ α × ∂ ϕ ∂ θ = i j k - b + a cos ⁡ θ cos ⁡ α b + a cos ⁡ θ cos ⁡ α 0 b + a cos ⁡ θ cos ⁡ α b + a cos ⁡ θ s e n   α a   s e n   θ

∂ ϕ ∂ α × ∂ ϕ ∂ θ = a b + a cos ⁡ θ cos ⁡ α cos ⁡ θ i + a b + a cos ⁡ θ sen ⁡ α cos ⁡ θ j + a   s e n   θ b + a cos ⁡ θ k

Assim, temos:

∂ ϕ ∂ α × ∂ ϕ ∂ θ = a b + a cos ⁡ θ cos ⁡ α cos ⁡ θ 2 + a b + a cos ⁡ θ sen ⁡ α cos ⁡ θ 2 + a   s e n   θ b + a cos ⁡ θ 2 ∴

∂ ϕ ∂ α × ∂ ϕ ∂ θ = a b + a cos ⁡ θ

Passo 5

Assim, aplicando na integral, temos:

A = 2 ∫ 0 2 π ∫ 0 2 π a b + a cos ⁡ θ   d α d θ ∴

A = 4 π 2 a b

Entendeu direitinho? Responde aee ;)

Resposta

ϕ α , θ = b + a cos ⁡ θ cos ⁡ α ,   b + a cos ⁡ θ   s e n   α , a   s e n   θ  

A = 4 π 2 a b

Exercícios de Livros Relacionados

(a) Se uma elipse é girada em torno de seu eixo maior, encontre o volume do sólido resultante.(b) Se ela for girada em torno de seu eixo menor, encontre o volume resultante.
Encontre a área da região delimitada pela hipérbole x 2 a 2 - y 2 b 2 = 1 e pela reta vertical passando por um foco.
Encontre a área da região dentro de um laco, onde r = s e n 2 θ .
Encontre a área da região que é limitada pelas curvas dadas e está no setor especificado: r = s e n ( θ ) ,π / 3 ≤ θ ≤ 2 π / 3
Esboce a área da região que está dentro de ambas as curvas. r = s e nθ ,r = cos ⁡ θ