Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Área de Curvas Parametrizadas

Ver Teoria
Exercício 5123467891011121314

Enunciado

UFMG, Sem Campus, Cálculo 2, Listas de Exercícios - Lista de Exercícios 5, Questão 1.9

Esboce o desenho da curva de equação polar

r = 2 + c o s ( 2 θ )

e calcule sua área

Passo 1

Fala pessoal, tudo beleza? Vamos para mais uma questão de Calc 2. Nosso objetivo é esboçar a curva

r = 2 + c o s ( 2 θ )

e calcular a sua área

Passo 2

queremos esboçar a curva polar

r = 2 + c o s ( 2 θ )

Vamos calcular alguns valores para a nossa curva

Quando θ = 0

r = 3

Quando θ = π / 6

r = 5 / 2

Quando θ = π / 2

r = 1

Quando θ = π

r = 3

juntando esses pontos e usando a simetria do cosseno, descobrimos que nossa curva é

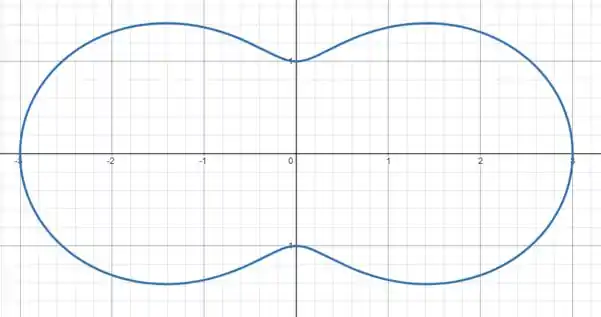
Passo 3

A área de uma curva polar é dada pela fórmula

A = 1 2 ∫ a b r 2 d θ

Nesse caso, nossa área será dada por

1 2 ∫ 0 2 π ( 2 + c o s ( 2 θ ) ) 2 d θ

= 1 2 ∫ 0 2 π 4 + 4 c o s ( 2 θ ) + c o s ( 2 θ ) 2 d θ

Integrando temos:

= 2 θ + s i n ( 2 θ ) + 1 2 ( 1 8 ( 4 θ - s i n ( 4 θ ) ) ) | θ = 2 π θ = 0

= 4 π   + π / 2

= 9 π / 2

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

D e s e n v o l v i m e n t o   A c i m a

Exercícios de Livros Relacionados

(a) Se uma elipse é girada em torno de seu eixo maior, encontre o volume do sólido resultante.(b) Se ela for girada em torno de seu eixo menor, encontre o volume resultante.
Encontre a área da região delimitada pela hipérbole x 2 a 2 - y 2 b 2 = 1 e pela reta vertical passando por um foco.
Encontre a área da região dentro de um laco, onde r = s e n 2 θ .
Encontre a área da região que é limitada pelas curvas dadas e está no setor especificado: r = s e n ( θ ) ,π / 3 ≤ θ ≤ 2 π / 3
Esboce a área da região que está dentro de ambas as curvas. r = s e nθ ,r = cos ⁡ θ