Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Área de Curvas Parametrizadas

Ver Teoria
Exercício 1234567891011121314

Enunciado

Encontre a área da elipse cuja equação paramétrica é x = 2 c o s t - 1   , y = 3 s e n t - 1   com 0 ≤ t ≤ 2 π

Passo 1

Vamos verificar se há trechos repetidos

Essa é a equação paramétrica de uma elipse. Como 0 ≤ t ≤ 2 π , essa elipse dá uma volta completa, ou seja, não há trechos repetidos ou sobrepostos.

Passo 2

Identificar qual dos 3 tipos de cálculo de áreas vamos usar.

Para isso, vamos observar seu gráfico. Essa é a equação de uma elipse com semi-eixos 2 e 3 e centro 1,1 . Seu gráfico é:

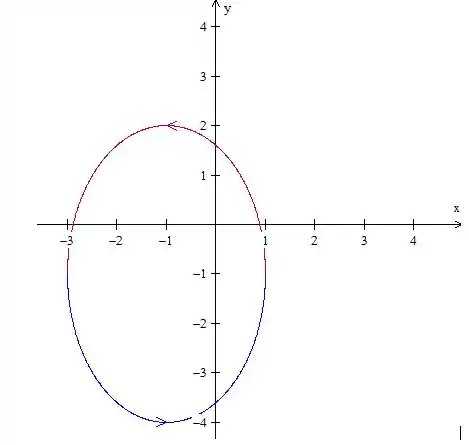
Bom, podemos dividir essa curva em dois segmentos: A parte em vermelho (parte de cima da curva), com equação x = 2 c o s t - 1   , y = 3 s e n t - 1 com 0 ≤ t ≤ π e a parte em azul (parte de baixo da curva), com equação x = 2 c o s t - 1   , y = 3 s e n t - 1 com π ≤ t ≤ 2 π .

Portanto, temos de calcular a área compreendida entre duas curvas.

Passo 3

Substituir as informações na integral para calcular a área.

A fórmula para calcular a área é:

A = ∫ A B [ f c i m a - f b a i x o ] d x = ∫ A B [ y c i m a - y b a i x o ] d x

Primeiramente, vamos começar identificando y c i m a e y b a i x o :

y c i m a = y b a i x o = 3 s e n t - 1

Agora, vamos encontrar d x :

x = 2 c o s t - 1

d x = - 2 s e n t d t

Falta definir os limites de integração

Vamos começar analisando a curva de cima. A integral relativa a ela é:

∫ A B y c i m a d x

Porém, repare que a curva não é orientada no sentido A → B , mas é percorrida de B para A . Portanto, os limites de integração serão trocados.

Para a curva de cima, t assume o valor de π no ponto A e 0 no ponto B . A integral fica:

∫ π 0 3 s e n t - 1 ( - 2 s e n t ) d t

Agora vamos analisar os limites de integração da curva de baixo. Ela percorre o sentido A → B , portanto os limites de integração são: π e 2 π . A integral fica:

∫ π 2 π 3 s e n t - 1 ( - 2 s e n t ) d t

A área é dada por:

A = ∫ π 0 3 s e n t - 1 - 2 s e n t d t - ∫ π 2 π 3 s e n t - 1 - 2 s e n t d t

Passo 4

Calcular a integral

Então vamos ter:

A = ∫ π 0 - 6 s e n 2 t + 2 s e n t d t - ∫ π 2 π - 6 s e n 2 t + 2 s e n t d t

Ajeitando temos:

A = ∫ π 0 - 6 1 - cos ⁡ 2 t 2 + 2 s e n t d t - ∫ π 2 π - 6 1 - cos ⁡ 2 t 2 + 2 s e n t d t

A = ∫ π 0 - 3 + 3 cos ⁡ 2 t + 2 s e n t d t - ∫ π 2 π - 3 + 3 cos ⁡ 2 t + 2 s e n t d t

Calculando as integrais:

A = - 3 t + 3 2 s e n 2 t - 2 cos ⁡ t 0 π - - 3 t + 3 2 s e n 2 t - 2 cos ⁡ t 2 π π

Temos:

A = 0 + 0 - 2 - - 3 π + 0 + 2 - - 6 π + 0 - 2 - - 3 π + 0 + 2  

A = 3 π - 4 + 6 π + 4 - 3 π

A = 6 π

Resposta

A = 6 π

Exercícios de Livros Relacionados

(a) Se uma elipse é girada em torno de seu eixo maior, encontre o volume do sólido resultante.(b) Se ela for girada em torno de seu eixo menor, encontre o volume resultante.
Encontre a área da região delimitada pela hipérbole x 2 a 2 - y 2 b 2 = 1 e pela reta vertical passando por um foco.
Encontre a área da região dentro de um laco, onde r = s e n 2 θ .
Encontre a área da região que é limitada pelas curvas dadas e está no setor especificado: r = s e n ( θ ) ,π / 3 ≤ θ ≤ 2 π / 3
Esboce a área da região que está dentro de ambas as curvas. r = s e nθ ,r = cos ⁡ θ