Uma chave de roda é usada para apertar um parafuso de cabeça quadrada. Se forças de forem aplicadas a chave, como mostrado, determine o módulo das forças iguais exercidas nos quatro pontos de contato na cabeça de do parafuso, de modo que seu efeito externo sobre o parafuso seja equivalente ao das duas forças de Considere que as duas forças são perpendiculares aos lados planos da cabeça do parafuso.
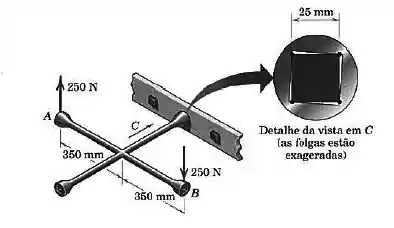
Passo 1
O sistema de forças inicial é esse aqui:
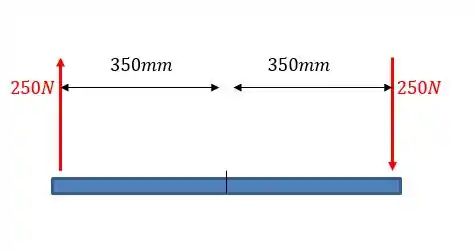
Não importa muito o sinal do momento. Queremos apenas saber depois quais forças vão gerar um torque equivalente a esse.
Assim, o momento, em módulo, pode ser calculado por:
Notou que multiplicamos por dois pois as duas forças giram a peça no mesmo sentido, né?
Passo 2
Agora o nosso sistema é esse aqui:
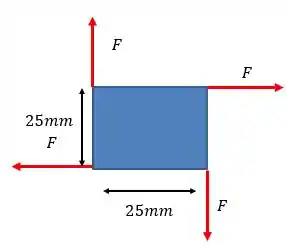
Beleza? Não sabemos o módulo de , mas sabemos que ela produz o mesmo torque que antes. Assim: