01) Na figura ao lado, os vértices determinam um cubo de lado . Aos vértices , e desse cubo aplicam-se as forças indicadas. Pede-se:
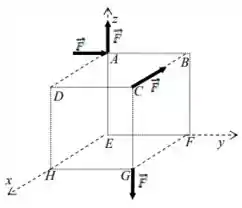
a) Determinar a resultante do sistema de forças;
b) determinar o momento resultante em relação ao polo ;
c) determinar o momento resultante em relação ao eixo ;
d) Verificar se o sistema é redutível a uma única força;
e) determinar o momento mínimo do sistema de forças.
Passo 1
Faaaala galerinha, tudo tranquilo com vocês?
Essa questão é bem legal, basicamente temos um cubo, de lado , sob a ação de forças de mesma intensidade em diferentes vértices.
a) Pra começar, devemos calcular a resultante de forças do sistema. A dificuldade é que as forças atuam em vértices diferentes, como a gente pode fazer nesse caso?

Então, não precisa se preocupar muito com isso. A ideia é escrever as forças vetorialmente, e somá-las eixo a eixo, sacaram?
Para o cubo em questão, temos:
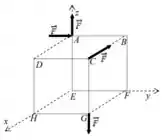
No vértice , temos:
Em :
Em
Somando esses resultados, vem:
Prontinho 😊
Passo 2
b) Nesse item devemos determinar o momento resultante das forças em relação ao polo . Lembra como podemos calcular, vetorialmente, o momento de uma força? Por exemplo, o momento que a força aplicada em realiza em , é dada por:
Sacou? Massa, então bora considerar a contribuição do momento que cada força realiza no polo . Daí:
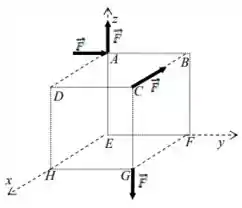
Excelente! Lembrando que o cubo possui lado . Vale que:
Substituindo esses dados no cálculo do momento, temos:
Logo:
Show de bola! Por fim, temos que o momento resultante no polo , , é dado por:
Substituindo, temos:
Aee, prontinho! Vamo pra próxima 😊
Passo 3
c) Devemos determinar o momento resultante em relação ao eixo .
O problema agora é que o momento é em relação a um eixo, como podemos calcular isso?

Sempre que queremos calcular o momento em relação a um eixo, podemos calcular o momento em relação a um dos pontos pertencentes a ele e tomar a componente do resultado na direção do próprio eixo.
Aqui, por exemplo, já calculamos o momento em relação ao ponto no item b). Daí:
Assim, agora basta pegarmos a componente desse resultado na direção do eixo , ou seja, na direção . Assim:
Prontinho, é só seguir esse passo a passo que vai dar certo 😉
Passo 4
d) Beleza gente, já estamos quase acabando. Nesse item, devemos verificar se o sistema é redutível a uma única força.
Pra um sistema ser redutível a uma única força precisamos que a força resultante e o momento resultante em um dado ponto sejam perpendiculares (ou ainda, que o momento seja nulo). Pra verificar essa perpendicularidade, costuma-se definir uma nova grandeza.
Quem tá lembrado do nome dela? haha

É o Invariante escalar! Ele é definido como:
Ou seja, um produto escalar. Se e forem perpendiculares, teremos . Aproveitando o resultado que já temos, podemos usar:
Do item a), temos também que:
Logo:
Logo, , o que implica no sistema não ser redutível a uma única força.
Passo 5
e) Nesse item devemos determinar o momento mínimo do sistema de forças.
Pra fazer isso, bora pensar na força e no momento resultantes no item e):
Beleza! Lembra que, quando a gente transporta uma força de um ponto para outro, isso gera também um momento no novo ponto?
Esse momento, é sempre perpendicular à força.
Assim, como queremos calcular o momento mínimo, o objetivo é pensar no ponto do sistema no qual não haja componente do momento perpendicular à força resultante, sacou?

Pensa comigo, se em um ponto P existir essa componente do momento perpendicular à resultante, é porque há algum outro ponto Q que, ao transportarmos a resultante pra gerou essa componente perpendicular. Sacou?
Resumindo, sempre que queremos calcular o momento mínimo é só calcular, para um ponto qualquer do sistema, a componente do momento resultante que é paralela à força resultante. Show?
Daí, a direção da força resultante é dada por:
Assim, pra calcular o momento mínimo, usando o ponto por exemplo, podemos fazer:
Logo, o vetor momento mínimo é dado por:
Bouaaa! Matamos mais uma questão gente. É isso aí!!
Espero que vocês tenham entendido bem direitinho, até a próxima 😉
Resposta
a)
b)
c)
d) Resolução no texto.
e)