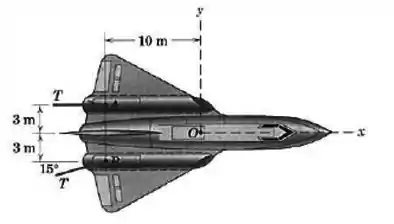
As direções dos dois vetores de empuxo de um avião experimental podem ser variadas independentemente, dentro de certos limites, desde a direção convencional à frente. Para a configuração de empuxo mostrada, determine o sistema força-binário equivalente no ponto Substitua, então, este sistema força-binário por uma única força e especifique sobre o eixo pela qual passa a linha de ação da resultante. Estes resultados são vitais para analisar o desempenho do projeto.
Passo 1
Para determinar o sistema equivalente força-binário, vamos calcular a força resultante e o momento resultante em relação ao ponto
Perceba que a força do propulsor de tem um braço de alavanca de , assim como a componente horizontal da força do propulsor de . Já a componente vertical da força de está distante do ponto . Adotando o sentido horário como o positivo, temos que:
Com a força e o momento, temos o sistema força-binário equivalente em
Passo 2
Vamos considerar que a barra abaixo representa o nosso avião. Quando calculamos o sistema força-binário equivalente no ponto , a configuração fica assim:
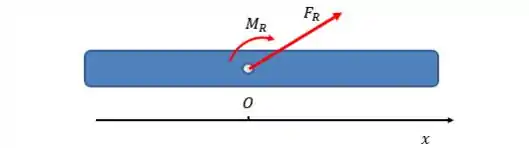
Ou seja, a força e o momento resultante ficam localizados em que é o nosso ponto de referência.
Agora queremos deslocar a força resultante ao longo de para que ela gere o mesmo momento que o binário gera.
Olhando para a figura, sabemos que ela precisa andar na direção negativa de (considerando que em , porque assim o momento terá sentido horário:
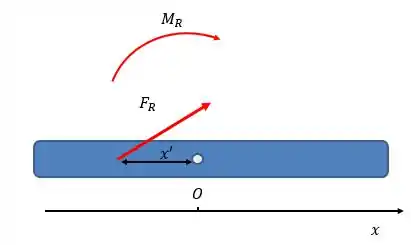
Além disso, apenas a componente em da força resultante () realizará momento, pois só ela terá um braço de alavanca.
Passo 3
Assim, podemos dizer que:
Por que o sinal de menos? Apenas para no final da conta ter um negativo. Ele precisa ser negativo, como vimos. Então:
Pronto!