Quatro pinos de de diâmetro são presos a uma tábua. Dois barbantes, apoiados nos pinos são tracionados, como ilustrado.
Determine o binário resultante na tábua.
Se apenas um barbante é usado, em quais pinos deverá ser apoiado e em que direções deverão ser tracionados a fim de que se produza o mesmo binário com uma força de tração mínima?
Qual o valor dessa força de tração mínima?
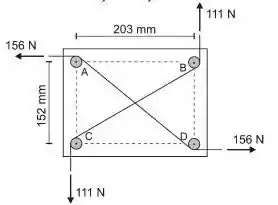
Passo 1
A resultante das forças é zero, afinal de contas, existem forças de mesmo módulo e sentidos contrários.
Em relação ao momento resultante, perceba que existem dois pares de forças que são igualmente espaçadas do centro da placa. Repare que a distância do ponto de aplicação da força até o centro do parafuso deve considerar o raio do parafuso. 25662
Assim, podemos calcular o momento resultante por:
Esse será o nosso momento do binário resultante:
Passo 2
Podemos apoiar em ou:
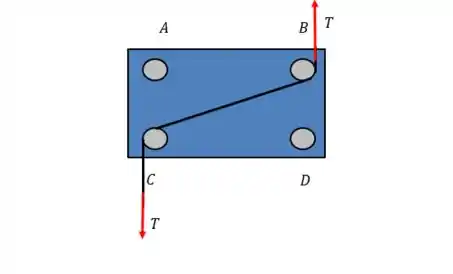
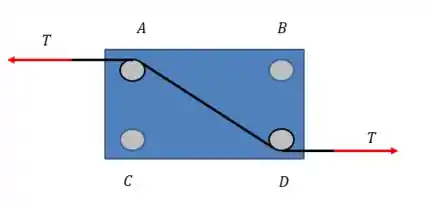
Os sentidos das tensões devem ser sempre contrários.
Passo 3
No caso de , a distância entre as forças vale . Assim:
Ou seja, o par de forças precisa exercer o mesmo momento que o binário, por isso a igualdade acima.
E no caso :
Assim, a tensão mínima vale e é gerada na configuração