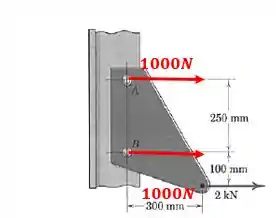
O suporte está preso a uma coluna por meio de dois rebites, e, e suporta uma força de . Substitua essa força por uma força atuando ao longo da mediatriz dos rebites e por um binário. Em seguida, redistribua essa força e o binário, substituindo-os por duas forças, uma em e outra em , e determine as forças suportadas pelos rebites.
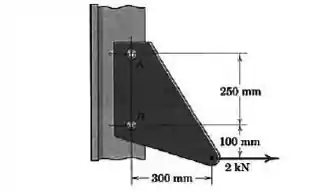
Passo 1
Para representar o sistema por um sistema força-binário, temos que calcular primeiro o momento que a força faz na mediatriz de .
Pra isso, temos que usar a distância entre o ponto de aplicação da força e a mediatriz de
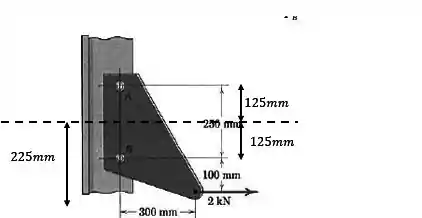
O momento é dado por:
Passo 2
Assim, o sistema binário-resultante é dado por:
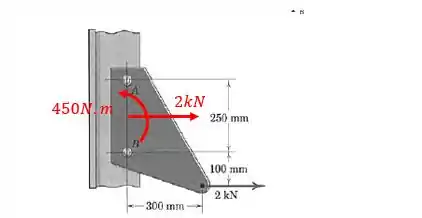
Passo 3
Pra redistribuir a força e o binário, primeiro vamos calcular o par de forças que sozinhas gerariam o momento desse binário:
Quem é essa distância? É a distância de cada parafuso até a mediatriz:
Entendeu o motivo de ser Ambas as forças giram no mesmo sentido:
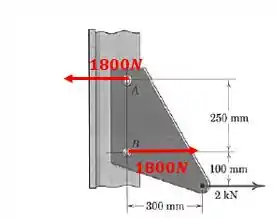
Passo 4
Já lidamos com o momento, agora precisamos lidar com a resultante das forças. Sabendo que ela vale , podemos dizer que em cada parafuso agem
Passo 5
Agora precisamos fazer a superposição dessas duas situações. Como? Somando as forças:
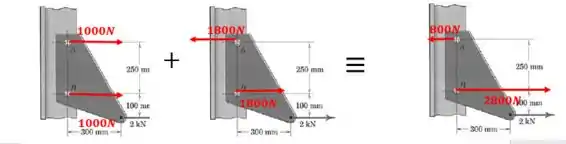
De acordo com os sentidos, teremos: