Duas polias estão submetidas às forças trativas das correias, como mostrado. Se a resultante destas forças passa pelo centro , determine , o módulo de e o ângulo anti-horário que faz com o eixo
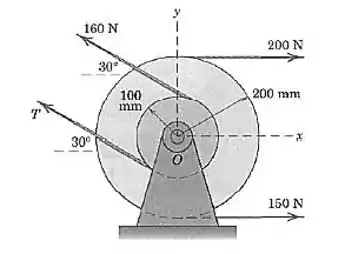
Passo 1
Quando a questão nos diz que a resultante das forças passa em um ponto, também está dizendo que o momento resultante naquele ponto é nulo.
Faz sentido né? Afinal de contas, se a combinação de todas as forças produz uma força que não exerce momento em certo ponto, é natural pensar que o momento resultante ali é nulo.
Então, o que sabemos é que:
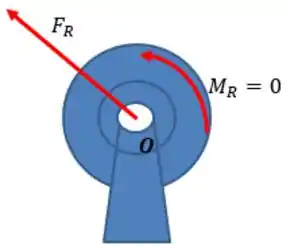
Passo 2
Assim, vamos calcular o momento que cada força exerce em relação ao ponto , somar tudo e igualar a zero (tomando o sentido horário como o positivo):
Show? Encontramos parte de nossa resposta.
Passo 3
Agora, de posse do módulo de , podemos calcular a resultante . Mas antes, vamos escrever cada força em termos de vetores e
- As forças de e
- e
Assim, é dado por:
Assim, o módulo de é dado por:
Passo 4
Falta a gente descobrir qual é o ângulo que faz com o eixo . Por enquanto, o que sabemos é que a resultante se localiza no primeiro quadrante, já que a componente horizontal e a vertical são positivas:
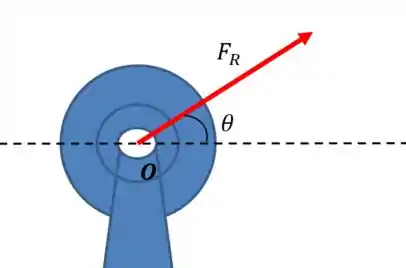
Podemos, então, calcular a tangente desse ângulo