01) Considere o sistema material indicado na figura, composto por uma placa plana ABCDEFGH, de espessura desprezível e uma barra vertical AI fixa rigidamente à placa. O sistema está livre no espaço. A placa plana é homogênea e tem peso . A barra vertical tem peso desprezível. Sobre o sistema material também atuam as seguintes forças: com , . Determine:
a) Mostre que o centro de massa da placa plana ABCDEFGH é o ponto M = .
b) A resultante e o momento resultante no ponto A.
c) A relação que deve existir entre P e Q para que o momento resultante em torno do eixo seja nulo.
d) A relação que deve existir entre P e Q para que o sistema de forças aplicadas possa ser reduzido a uma única força.
e) O momento mínimo do sistema de forças, considerando que P e Q satisfaçam a relação obtida no item anterior.
Passo 1
Faaaala pessoal, tudo certinho com vocês?
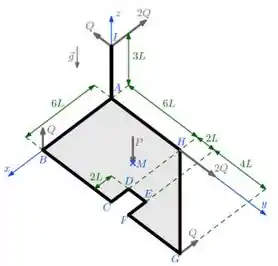
a) Para começar, precisamos encontrar o centro de massa da placa ABCDEFGH. Nesse tipo de questão, a principal ideia é dividir a placa em partes conhecidas da geometria (quadrados, triângulos, retângulos) para calcularmos o seu CM. Isso porque, como a placa é homogênea, podemos dizer que:
Onde é a área total da placa plana ABCDEFGH.
Daí, para determinar , temos:
Para o a equação é análoga.
Beleza, então vamos dividir em 3 partes interessantes:
O quadrado ABCH, o furo quadrado CDEF e o triângulo retângulo CGH.
Lembrando que o furo quadrado é considerado como tendo “área negativa”, já que na verdade não há pedaço da placa nessa região, mas estamos considerando esse pedaço no triângulo CGH
O quadrado e o furo quadrado possuem seu e localizados bem no meio da sua geometria, devido à simetria.
Já o triângulo retângulo tem o CM localizado no seu baricentro, que fica a 1/3 da altura e 1/3 da base.
Assim, podemos montar a seguinte tabela:
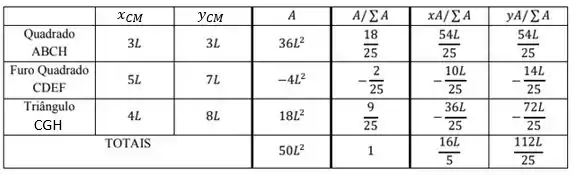
Prontinho, encontramos que e .
Como a placa é plana, .
Portanto, o CM da placa se localiza no ponto M = .
Passo 2
b) Bom, nesse item precisamos determinar a resultante das forças e o momento resultante atuando em A.
É importante lembrar que pra transportar uma força para outro ponto da placa, precisamos contabilizar o momento que ela faz naquele ponto. Assim, pegando por exemplo a força peso que atua no ponto M. A contribuição dela na resultante das forças é o próprio . Mas, a contribuição dela na resultante dos momentos em A, precisa ser calculada:
Perceberam a ideia? Podemos pegar o braço de cada força em cada um dos eixos pra fazer os respectivos produtos vetoriais. Depois de realizar todos os produtos vetoriais, só precisamos somá-los.
Bora fazer isso montando uma tabelinha, vai ficar assim:
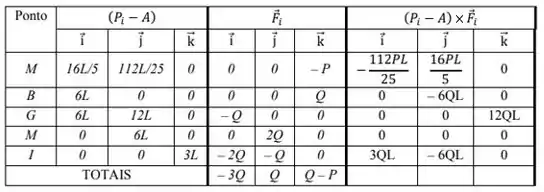
Massa! Agora é só somarmos:
Somando os momentos, temos:
Prontinho! Lá foi mais uma letra. Vamo pra próxima!
Passo 3
c) Precisamos determinar a relação entre e para que o momento em relação ao eixo seja nulo. O bom é que já calculamos o momento resultante em A, daí o eixo é simplesmente a componente em de . Assim:
Logo:
Portanto, precisamos ter:
Prontinho 😊
Passo 4
d) Precisamos determinar a relação entre e para que o sistema possa ser reduzido a uma única força. Mas o que significa ser redutível a uma única força? Significa que o invariante escalar é nulo, ou seja, o momento resultante em A é perpendicular à força resultante no mesmo polo.
Matematicamente, podemos expressar essa condição por:
Usando os valores que encontramos no item B, temos que:
Excelente!! Já matamos mais uma letra, falta só mais uma.
Passo 5
e) Neste item devemos determinar o momento mínimo considerando que e obedecem à relação do item D. Ou seja, o momento mínimo quando o nosso sistema de forças é redutível a uma única força.Mas, pensa comigo, se podemos reduzir o sistema inteiro a uma única força, escolhendo como polo o ponto de aplicação dessa força, teremos o momento mínimo nulo.É exatamente isso, como podemos reduzir o sistema a uma única força, o momento mínimo na placa é nulo!
Ufaa! Mais uma questão terminada. Espero que vocês tenham conseguido entender direitinho. Até a próxima galera, tamo junto!
Resposta
a) Resolução no texto.
b)
c)
d)
e) Resolução no texto.