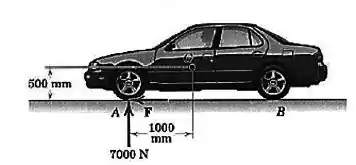
As rodas do automóvel de tração dianteira sofrem, em conjunto, a ação de uma força de reação normal de e de uma força de fricção , ambas exercidas pela superfície da estrada. Se é sabido que a resultante destas forças faz um ângulo de com a vertical, determine o sistema força-binário equivalente no centro de massa do carro. Trate esse problema como sendo bidimensional.
Passo 1
A força resultante faz um ângulo de com a vertical:
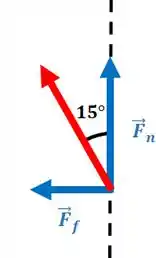
Nós sabemos quem é , mas não sabemos quem é . Porém, podemos usar:
Passo 2
Assim, o módulo da força resultante vale:
E a força resultante pode ser escrita como:
Passo 3
Agora precisamos calcular o momento resultante. Para isso, vamos usar as componentes separadamente:
A componente friccional está a de , então:
E a componente normal está a de
Ambas as forças fazem o corpo girar no mesmo sentido, então:
Assim, o sistema equivalente força-binário em tem as seguintes características: